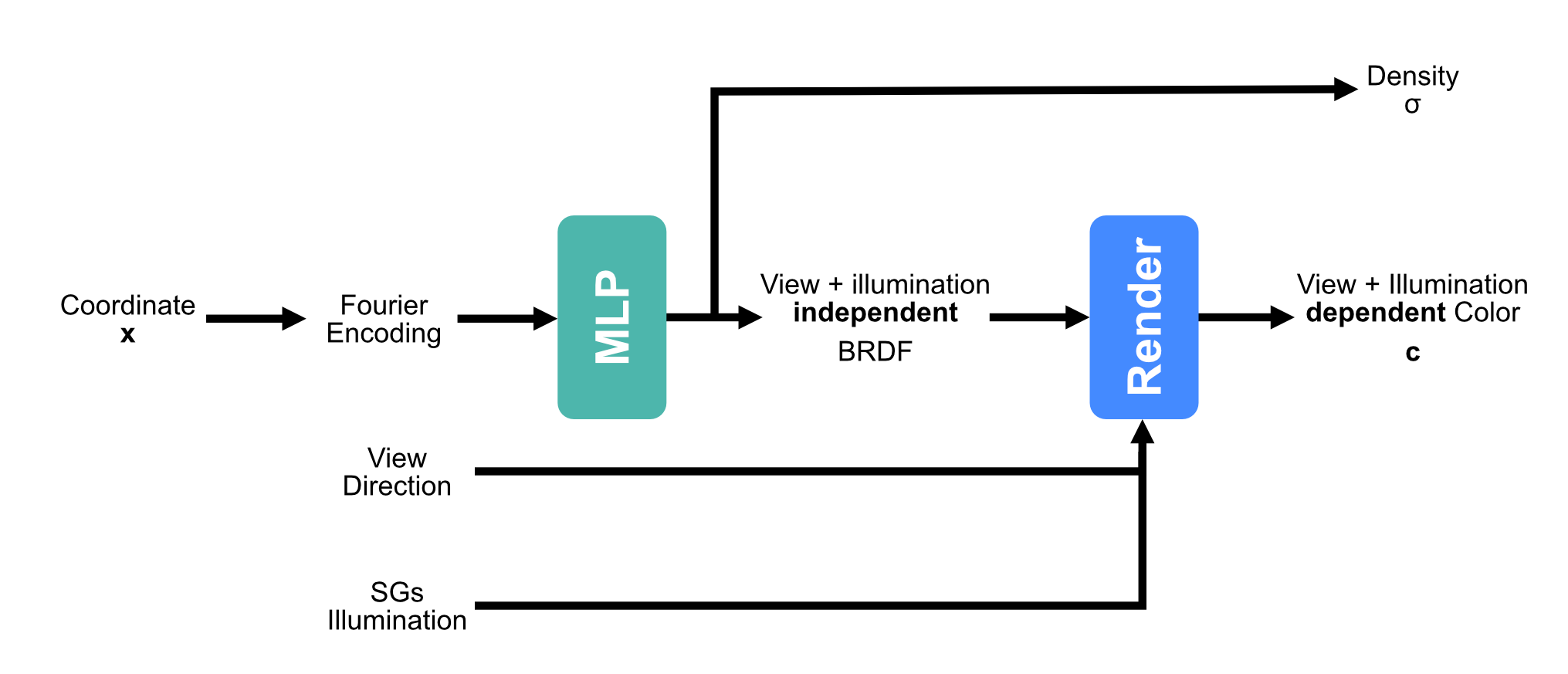
Neural Reflectance Decomposition

Extracting BRDF, shape, and illumination from images using inverse rendering

Presented By
Mark Boss
Goal - Teaser

Multiple input images (potentially multiple illuminations)

Relightable 3D asset from our work [1]

[1] Result from: Boss et al. - NeRD: Neural Reflectance Decomposition from Image Collections - 2021

Contributions - Optimization Targets

Shape

Appearance

Illumination

Pose

Contributions - Result Capabilities

Novel view synthesis

Relighting

Downstream applications

Contributions - Data Constraints

Varying & fixed illumination

Objects in varying locations

No segmentation masks

Applications

Games

Movies

AR/VR

Virtual shopping

Background

Rendering

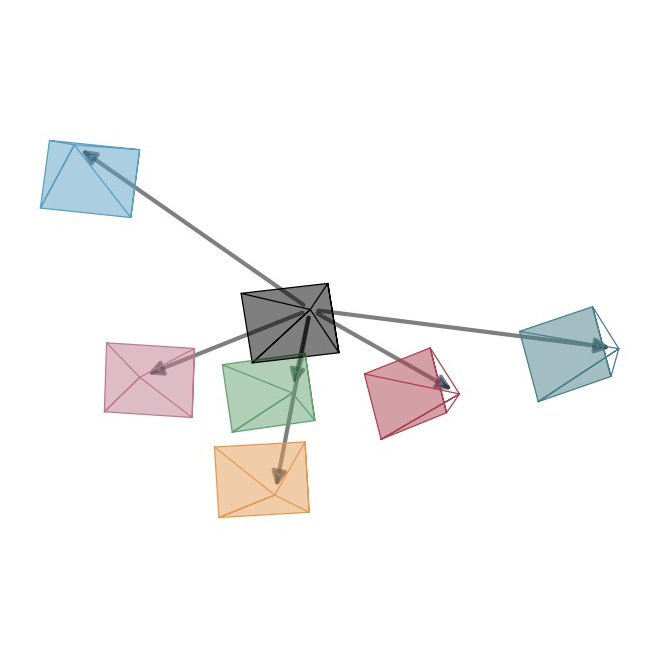
[1] James T. Kajiya - The Rendering Equation - 1986

Rendering equation [1]

$$ \definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,= \fragment{1}{\,\color{emit}L_{e}({\mathbf x},\,\omega_{o})} \fragment{2}{\color{black} + \\ \color{int}\int_{\Omega }} \fragment{4}{\color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o})} \fragment{3}{\color{in}L_{i}({\mathbf x},\,\omega_{i})}\, \fragment{5}{\color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})}\, \fragment{2}{\color{int}\operatorname d\omega_{i}}$$

Simplification: No self-emittance

$$ \definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,=\,\color{int}\int_{\Omega} \color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) \\ \color{in}L_{i}({\mathbf x},\,\omega_{i})\, \color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})\, \color{int}\operatorname d\omega_{i}$$

Infinitely Far Illumination

$$ \definecolor{point}{RGB}{232,0,19} L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\color{point}{\mathbf x}\color{black},\,\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$

Simplification: Illumination only dependent on direction

$$L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$

Workshop Metaphor [1]

Image

Sculptor

Painter

Gaffer

Possible explanation

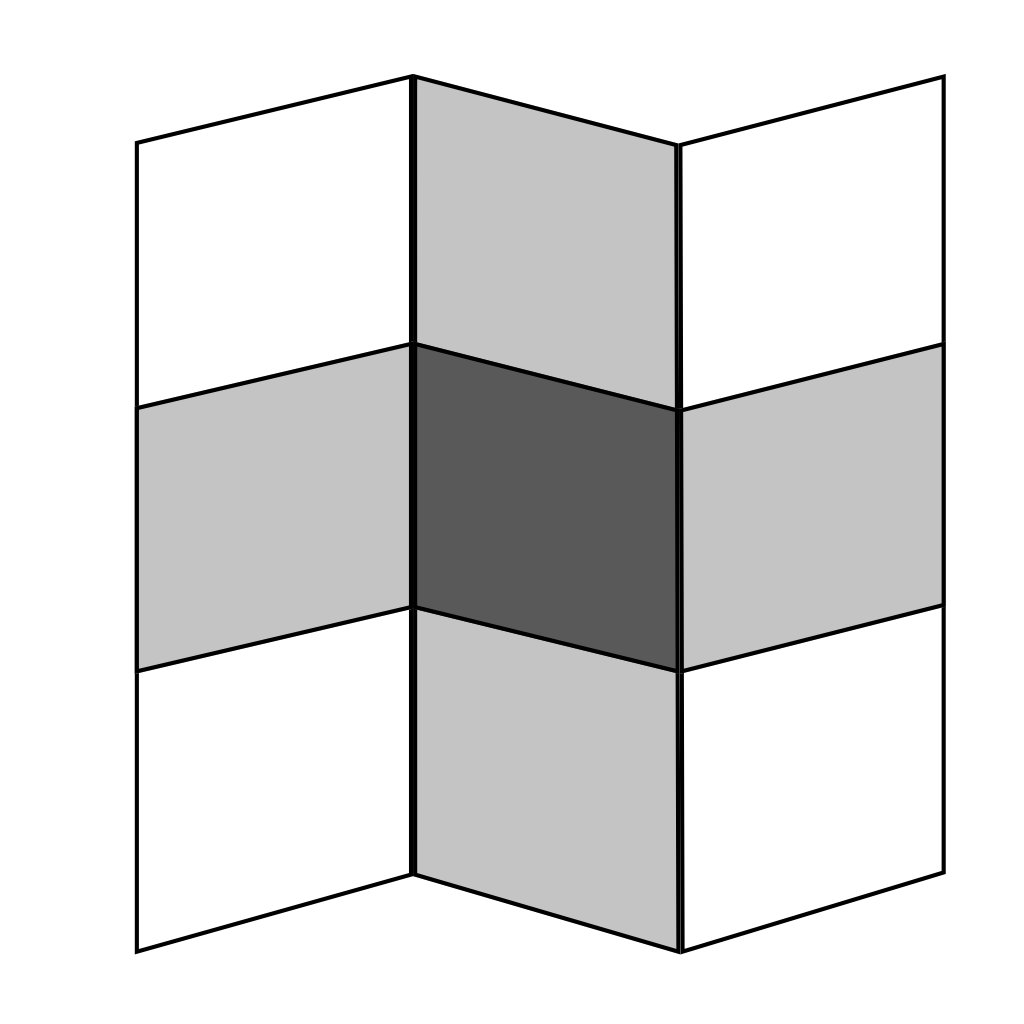
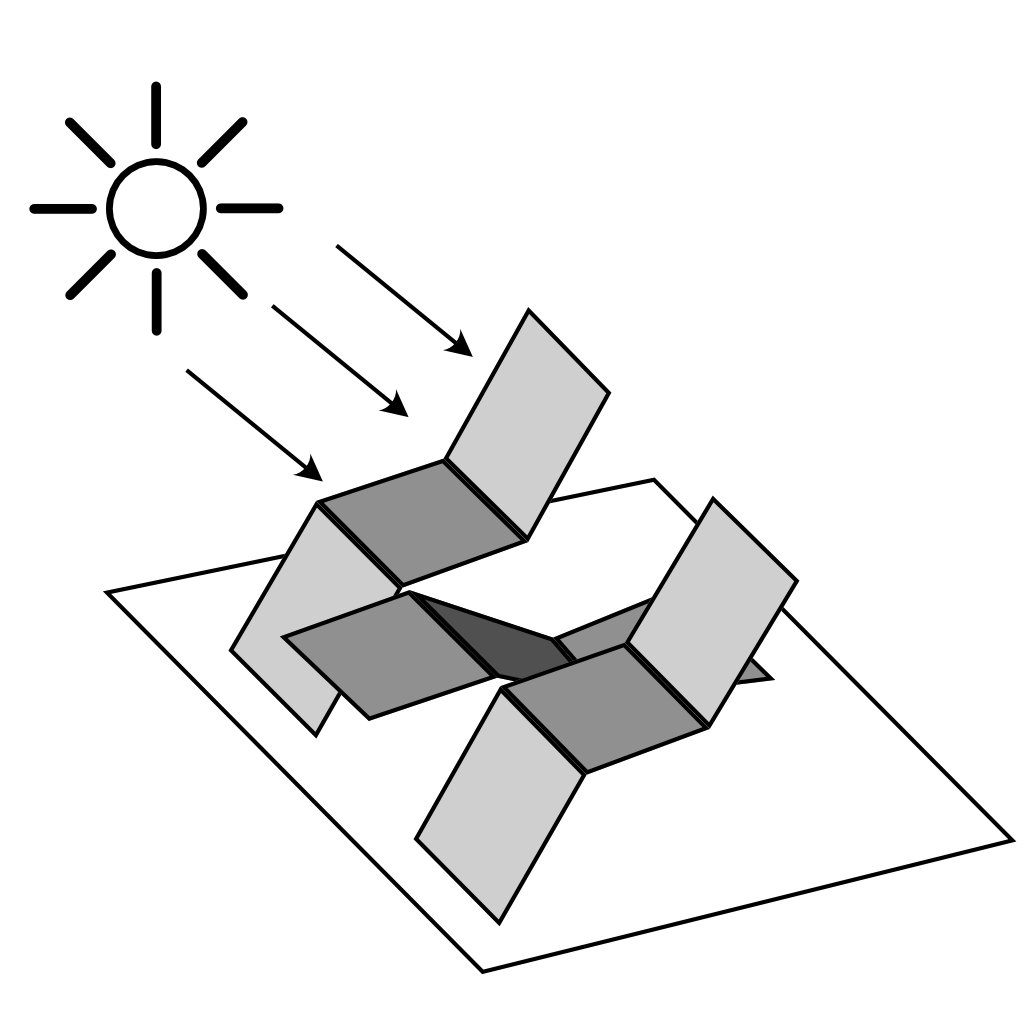
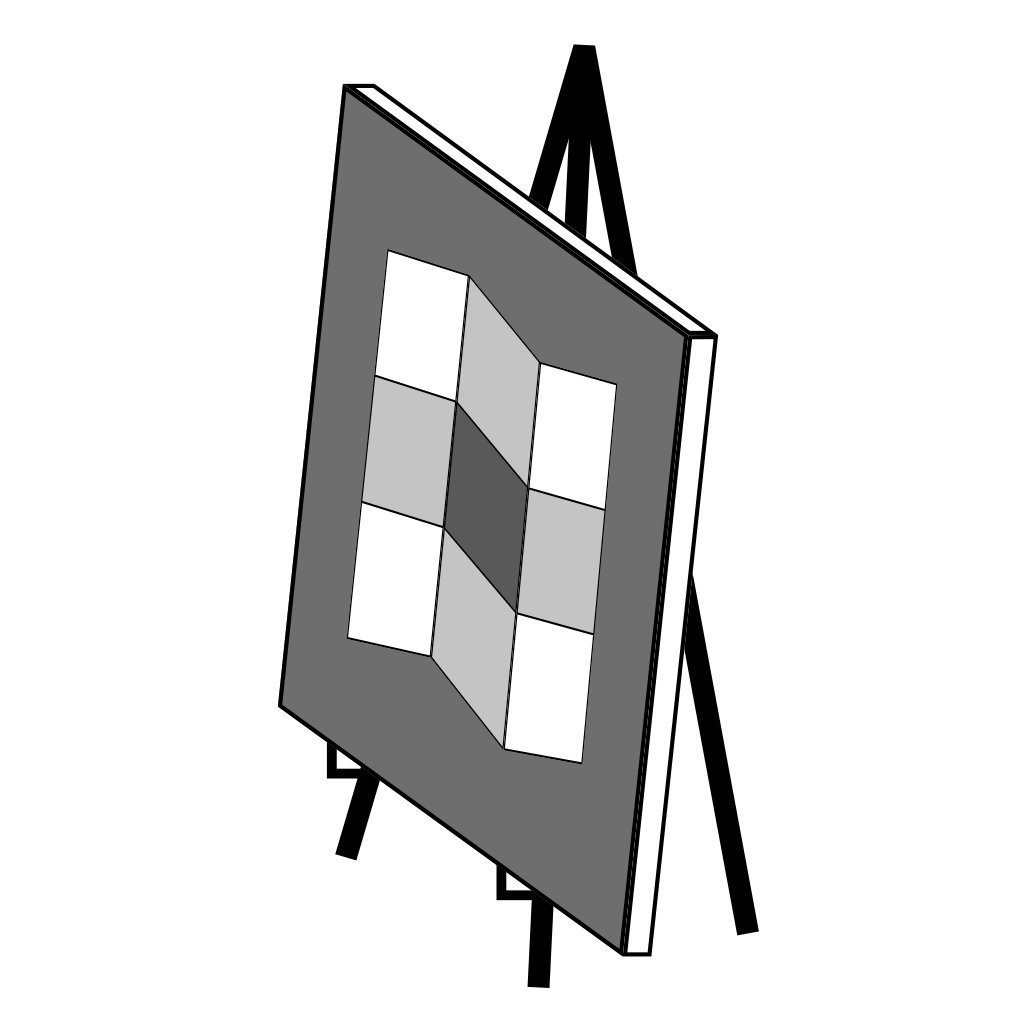
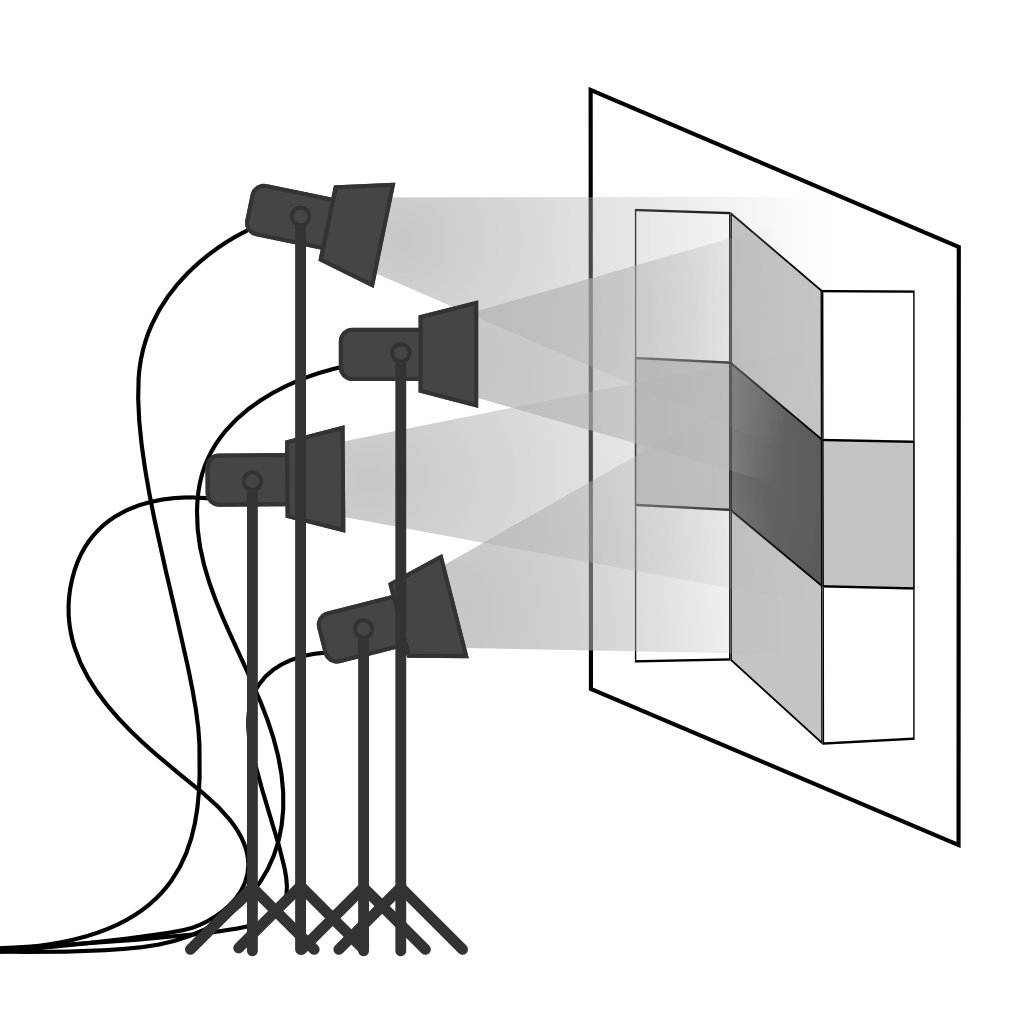
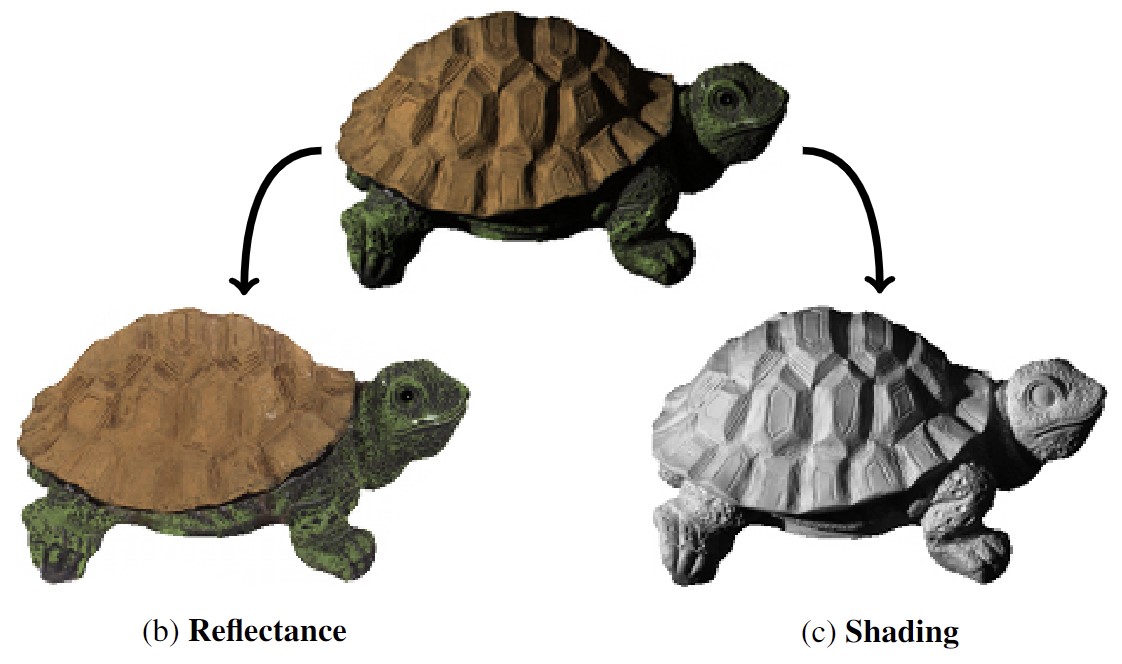
[1] E.H. Adelson, A.P. Pentland - The Perception of Shading and Reflectance - 1996

Inverse Rendering

Plenoptic function

  • Main use-case: novel view synthesis
  • Estimate the view-dependent color
  • No relighting possible

Intrinsic image

  • Splits an image into layers
  • Layers have no physical meaning
  • Limited relighting possible

Full decomposition

  • Decomposes the rendering equation
  • Appearance modelled as BRDF
  • Illumination as incoming radiance
  • Fully relightable

Preliminaries - NeRF

NeRF: Neural Radiance Fields
  • NeRF [1] is a method for photorealistic results in novel view synthesis
  • Goal is to create a 3D radiance field from multiple images
  • Images have known poses

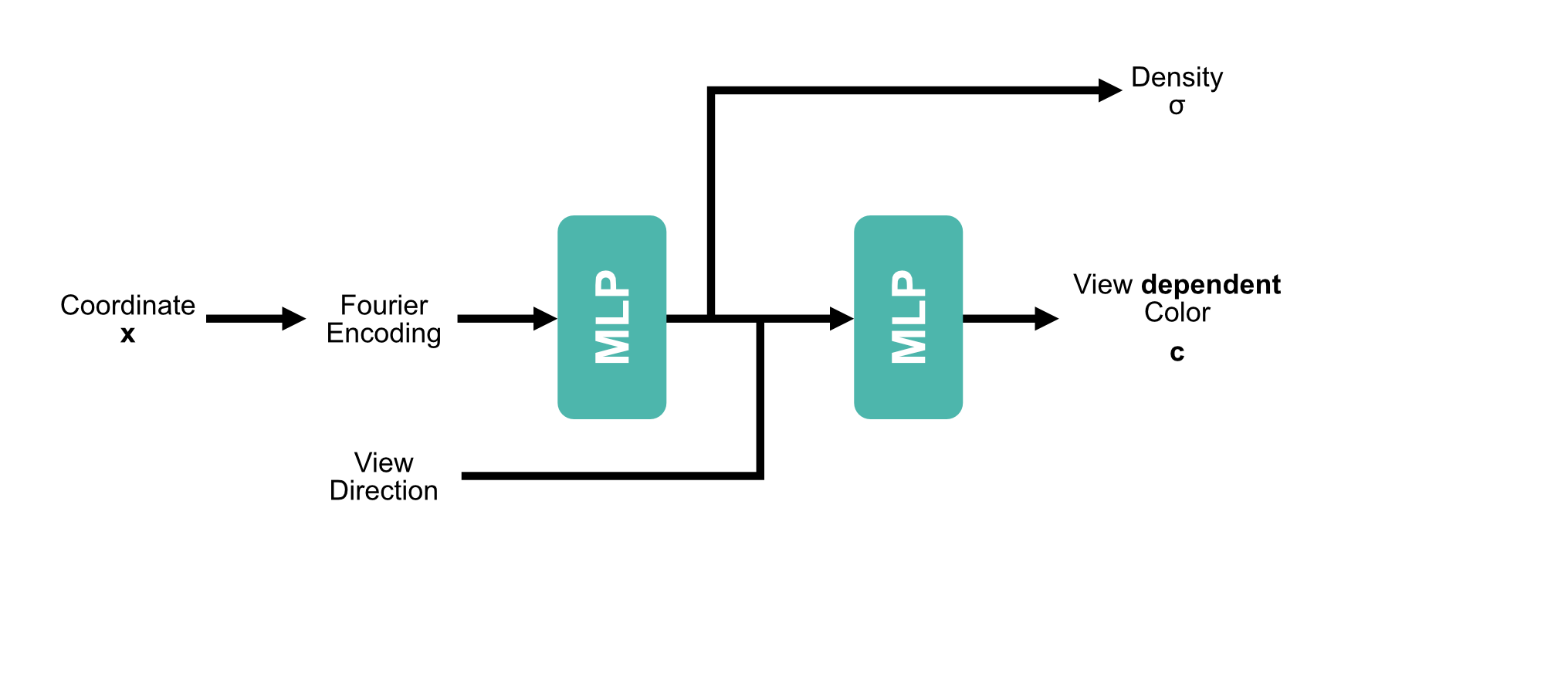
[1] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

NeRF - Visualization
NeRF - Architecture
  • Main section of NeRF learns density and latent code
  • Last layers of NeRF estimates view-dependent color
    • Shape should not be influenced by the viewing direction
  • NeRF is not relightable

View dependence with NeRF

NeRF architecture

Fourier encoding

  • Sinusoidal embedding with increasing frequencies

$$\gamma(x) = (\sin(2^l x))^{L-1}_{l=0}$$

NeRF - Varying Illumination Extension
  • Assume dataset of 4 images
  • Images under varying illumination

NeRF architecture

NeRF-A architecture

Potential solution

  • Use additional latent code to express each illumination
  • Interpolate between illuminations
Illumination Interpolation
Issues with Illumination Interpolation
  • Only interpolate between seen illuminations
  • No issue if dataset is vast and contains all possible illuminations
  • However, it is hard to get all possible illumination edge cases

Illumination at night

Full Decomposition - Our Method [1]

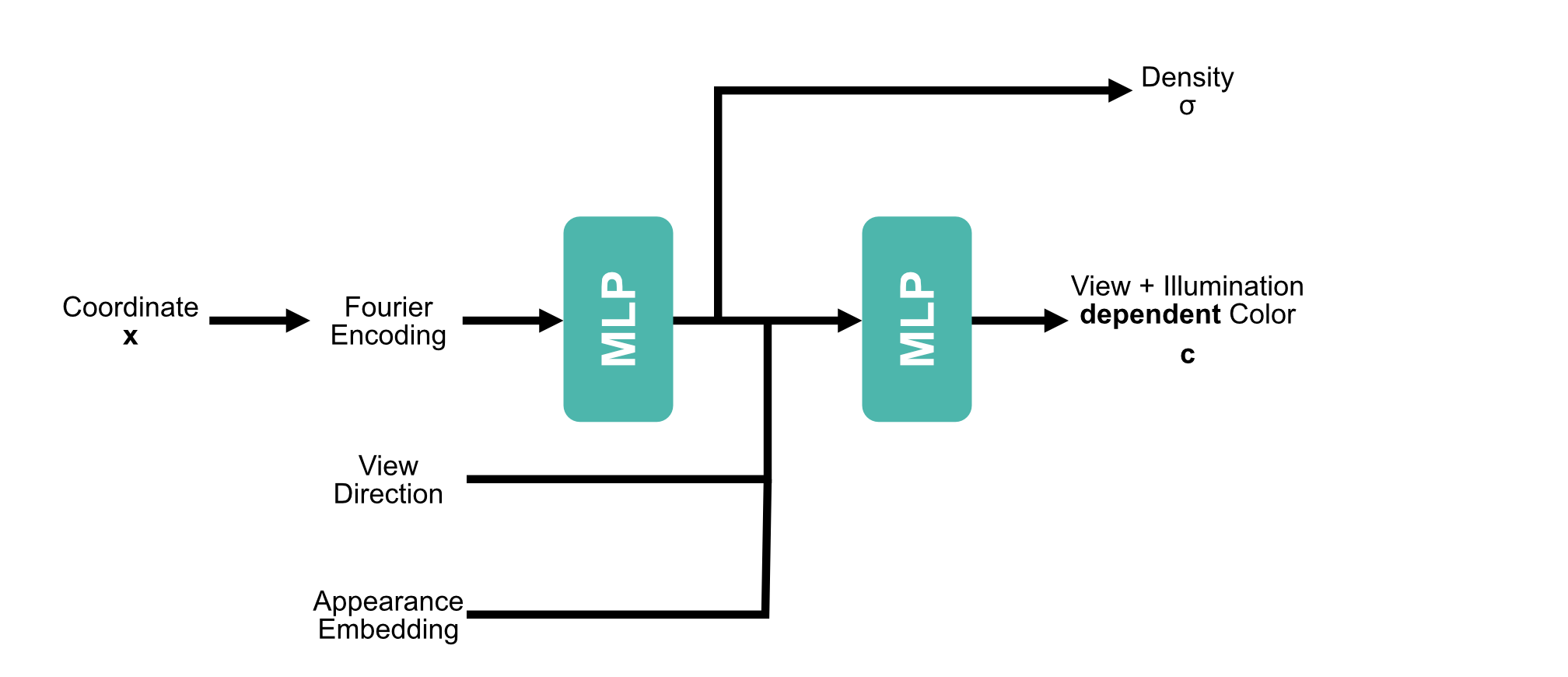
[1] Boss et al. - NeRD: Neural Reflectance Decomposition from Image Collections - 2021

Methods

NeRD: Neural Reflectance Decomposition from Image Collections

Mark Boss, Raphael Braun, Varun Jampani, Jonathan T. Barron, Ce Liu, Hendrik P. A. Lensch
IEEE International Conference on Computer Vision 2021
Contributions
Method Shape Appearance Light Pose Novel View Relightable Down- stream Varying Light Varying Locations No Masks
NeRF [1] ✔ ✔ ❌ ❌ ✔ ❌ ✱ ❌ ❌ ✔
NeRF-W [2] ✔ ✔ ✱ ❌ ✔ ✱ ✱ ✔ ❌ ✔
NeRV[3], PhySG[4], NvDiffRec[5] ✔ ✔ ✔ ❌ ✔ ✔ ✔ ❌ ❌ ❌
NeRD ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌

[1] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

[2] Martin-Brualla et al. - NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections - 2021

[3] Srinivasan et al. - NeRV: Neural Reflectance and Visibility Fields for Relighting and View Synthesis - 2021

[4] Zhang et al. - PhySG: Inverse Rendering with Spherical Gaussians for Physics-based Material Editing and Relighting - 2021

[5] Munkberg et al. - Extracting Triangular 3D Models, Materials, and Lighting From Images - 2022

Amplifying NeRF for Full Relighting

NeRF-A architecture

NeRD architecture

Spherical Gaussians

Rendering equation

$$L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$

  • Rendering requires integrating all incoming light
  • Spherical Gaussian (SG) have convenient properties
  • Close-form solution exists for integration 2 SGs
  • Product of 2 SGs is a SG


  • Represent illumination and BRDF as SGs
  • Closed form integration enables fast rendering
    • No sampling noise compared to Monte Carlo integration

Polar plot of 1D Gaussian

Specular lobe of BRDF

Downstream: Mesh Extraction
  • Extracting textured meshes allows multiple use cases
Results
Comparisons - Single Illumination

Input

Comparisons - Single Illumination

GT

NeRF

NeRD

Results - Novel View Synthesis

Synthetic scenes - PSNR
Method Single Multiple
NeRF 34.24 21.05
NeRF-A 32.44 28.53
NeRD (Ours) 30.07 27.96

Real world scenes - PSNR
Method Single Multiple
NeRF 23.34 20.11
NeRF-A 22.87 26.36
NeRD (Ours) 23.86 25.81

Neural-PIL: Neural Pre-Integrated Lighting for Reflectance Decomposition

Mark Boss, Varun Jampani, Raphael Braun, Ce Liu, Jonathan T. Barron, Hendrik P. A. Lensch
Advances in Neural Information Processing Systems 2021
Contributions
Method Shape Appearance Light Pose Novel View Relightable Down- stream Varying Light Varying Locations No Masks
NeRF [1] ✔ ✔ ❌ ❌ ✔ ❌ ✱ ❌ ❌ ✔
NeRF-W [2] ✔ ✔ ✱ ❌ ✔ ✱ ✱ ✔ ❌ ✔
NeRV[3], PhySG[4], NvDiffRec[5] ✔ ✔ ✔ ❌ ✔ ✔ ✔ ❌ ❌ ❌
NeRD ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌
Neural-PIL ✔ ✔+ ✔+ ❌ ✔+ ✔+ ✔+ ✔ ❌ ❌

[1] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

[2] Martin-Brualla et al. - NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections - 2021

[3] Srinivasan et al. - NeRV: Neural Reflectance and Visibility Fields for Relighting and View Synthesis - 2021

[4] Zhang et al. - PhySG: Inverse Rendering with Spherical Gaussians for Physics-based Material Editing and Relighting - 2021

[5] Munkberg et al. - Extracting Triangular 3D Models, Materials, and Lighting From Images - 2022

Issues with Spherical Gaussians
Pre-Integrated Illumination [1]
  • Pre-compute light integrals for fast rendering

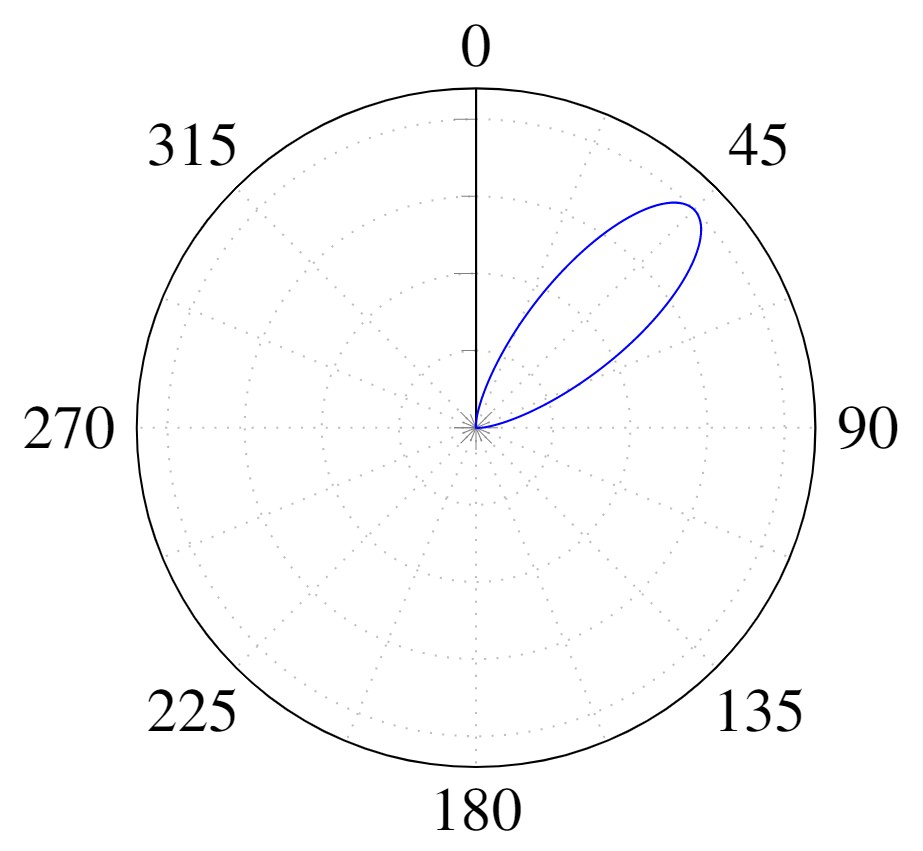
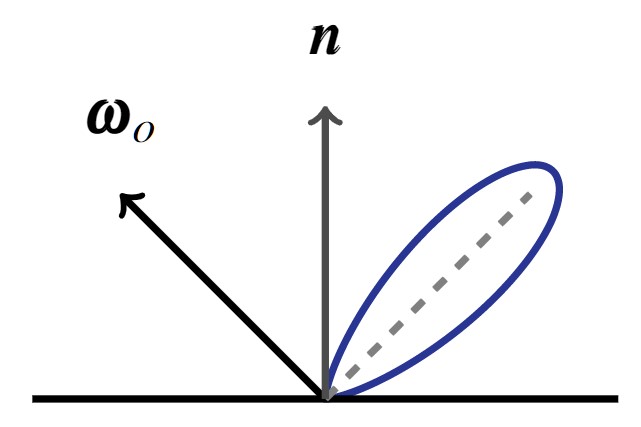
$L_o(x,\omega_o) = \underbrace{\frac{c_d}{\pi} \int_\Omega L_i(x, \omega_i) (\omega_i \cdot n) d\omega_i}_{\text{Diffuse}} + \underbrace{\int_\Omega f_r(x,\omega_i,\omega_o; c_s, c_r) L_i(x, \omega_i)(\omega_i \cdot n) d\omega_i}_{\text{Specular}}$

$L_o(x,\omega_o) = \underbrace{\frac{c_d}{\pi} \color{red}\boxed{\color{black}\int_\Omega L_i(x, \omega_i)}\color{black} (\omega_i \cdot n) d\omega_i}_{\text{Diffuse}} + \underbrace{\color{red}\boxed{\color{black}\int_\Omega}\color{black} f_r(x,\omega_i,\omega_o; c_s, c_r) \color{red}\boxed{\color{black}L_i(x, \omega_i)}\color{black} (\omega_i \cdot n) d\omega_i}_{\text{Specular}}$

Pre-integrated light formulation

$$\color{red}\boxed{\color{black}\tilde{L}_i(\omega_r, c_r)}\color{black} = \int_\Omega D(c_r, \omega_i, \omega_r)L_i(x, \omega_i)d\omega_i$$

Pre-integrated rendering equation

$$L_o(x,\omega_o) \approx \underbrace{\frac{c_d}{\pi} \tilde{L}_i(n, 1)}_{\text{Diffuse}} + \underbrace{b_s (F_0(\omega_o,n)B_0(\omega_o \cdot n, c_r) + B_1(\omega_o \cdot n, c_r)) \tilde{L}_i(\omega_r, c_r)}_{\text{Specular}}$$

→ Simple set of additions and multiplications

[1] Karis et al. - Real Shading in Unreal Engine 4

Pre-Integrated Illumination [1]

[1] Karis et al. - Real Shading in Unreal Engine 4

Neural-PIL
  • Light pre-integration is computed with brute-force (expensive)
  • We need to do the pre-integration on the fly
  • Neural-PIL that converts light pre-integration into a simple network query
  • Architecture based on pi-GAN [1]

Evaluation time
Rendering SGs Neural PIL
1 Million Samples 0.21s 0.00186s

SGs vs. Monte-Carlo vs. Neural-PIL

[1] Chan et al. – pi-GAN: Periodic Implicit Generative Adversarial Networks for 3D-Aware Image Synthesis - 2021

Smooth Manifold Prior
  • Constraints BRDF and light to plausible values
  • Use frozen decoders during decomposition - only optimize latent code
  • Smooth latent manifold crucial for following optimization
  • Explicit latent space interpolation during training
  • Losses to encourage smooth manifold formation:
    • Adversarial
    • Gradient regularization during manifold interpolation

Smooth manifold training

BRDF SMAE Smoothness
Comparisons - Single Illumination

Input

Comparisons - Single Illumination

GT

NeRF

NeRD

Neural-PIL

Multiple Illumination Reconstruction

Examplary input

Examplary input

Examplary input

Results

Synthetic scenes - PSNR
Method Single Multiple
NeRF 34.24 21.05
NeRF-A 32.44 28.53
NeRD (Ours) 30.07 27.96
Neural-PIL (Ours) 30.08 29.24

Real world scenes - PSNR
Method Single Multiple
NeRF 23.34 20.11
NeRF-A 22.87 26.36
NeRD (Ours) 23.86 25.81
Neural-PIL (Ours) 23.95 26.23

SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections

Mark Boss, Andreas Engelhardt, Abhishek Kar, Yuanzhen Li, Deqing Sun, Jonathan T. Barron, Hendrik P. A. Lensch, Varun Jampani
Advances in Neural Information Processing Systems 2022
Traditional Pose Recovery Fails

Main Idea

  • Move previous methods to real-world online collections
  • Traditional pose estimation failed on these datasets
  • No features can be used in backgrounds and foreground vary too much
Contributions
Method Shape Appearance Light Pose Novel View Relightable Down- stream Varying Light Varying Locations No Masks
NvDiffRec [1] ✔ ✔ ✔ ❌ ✔ ✔ ✔ ❌ ❌ ❌
NeRD ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌
Neural-PIL ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌
BARF [2] ✔ ✔ ❌ ✔ ✔ ❌ ✱ ❌ ❌ ✱
GNeRF [3] ✔ ✔ ❌ ✔ ✔ ❌ ✱ ❌ ❌ ✱
SAMURAI ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✱

[1] Munkberg et al. - Extracting Triangular 3D Models, Materials, and Lighting From Images - 2022

[2] Lin et al. - BARF: Bundle-Adjusting Neural Radiance Fields - 2021

[3] Meng et al. - GNeRF: GAN-based Neural Radiance Field without Posed Camera - 2021

Decomposition from Coarsely Posed Images
Coarse-to-Fine & Camera Multiplex
  • Fourier Encoding Annealing from BARF [1]
    • Increases encoding frequencies during training
    • Higher $L$ are blended in
    • Smooth shapes easier to align

Positional encoding

$$\gamma(x) = (\sin(2^l x))^{L-1}_{l=0}$$

  • Gradual increase in resolution
  • Multiple camera estimates
    • Posterior scaling only allows best camera to optimize volume

Coarse-to-fine during training

[1] Lin et al. - BARF: Bundle-adjusting neural radiance fields

Camera Multiplex
Image Posterior Scaling
  • Posterior scaling also applied on image level
  • Influence of badly aligned images or segmentation masks reduced
  • Scaling based on running average of losses

Influence of poorly aligned images is reduced

Results
Results
Comparison with BARF

Exemplary Inputs

BARF

SAMURAI

NeRF View Conditioning

NeRF architecture

Frozen position with view conditioning

BARF Conditioning Entanglement

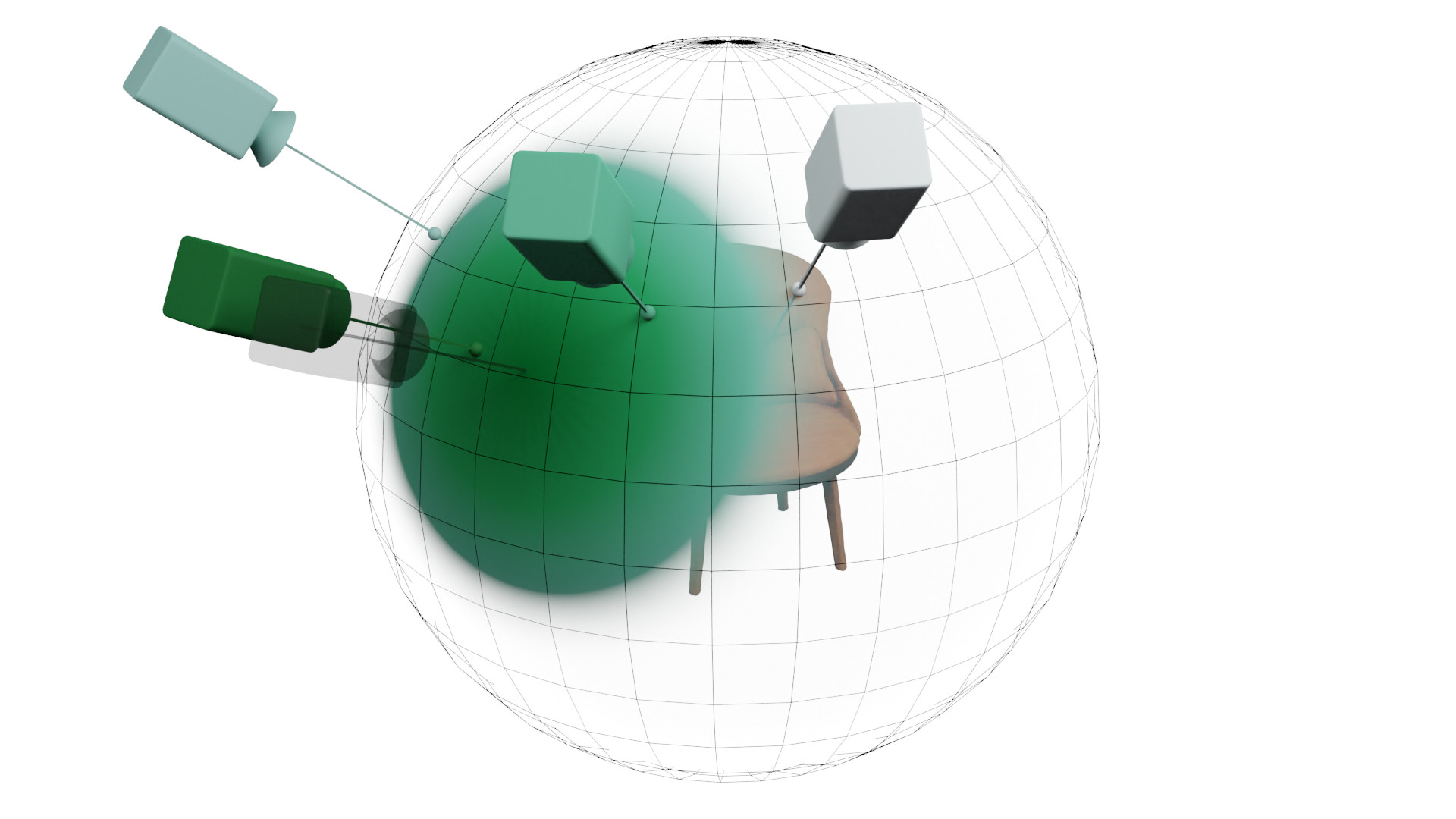
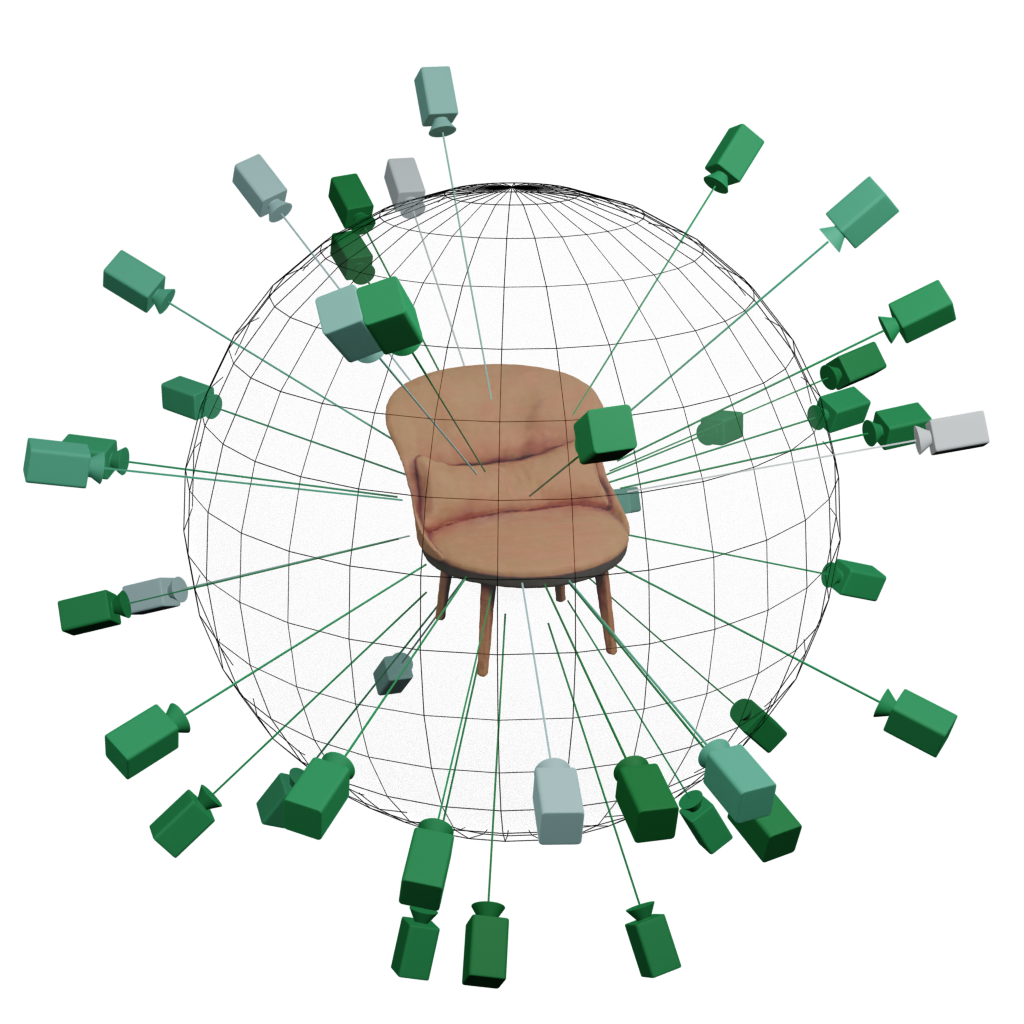
Moving Camera

BARF

SAMURAI

View Conditioning

 

 

Results - Novel View Synthesis

Single Illumination
Method Pose Init PSNR ↑ Translation Error ↓ Rotation° Error ↓
BARF [1] Quadrants 14.96 34.64 0.86
GNeRF [2] Random 20.3 81.22 2.39
NeRS [3] Quadrants 12.84 32.77 0.77
SAMURAI Quadrants 21.08 33.95 0.71
NeRD GT 23.86 — —
Neural-PIL GT 23.95 — —

[1] Lin et al. - BARF: Bundle-adjusting neural radiance fields

[2] Meng et al. - GNeRF: GAN-based Neural Radiance Field without Posed Camera

[3] Zhang et al. - NeRS: Neural reflectance surfaces for sparse-view 3d reconstruction in the wild

Results - Novel View Synthesis & Relighting

Dataset with poses available (NeRD datasets)
Method Pose Init PSNR ↑ Translation Error ↓ Rotation° Error ↓
BARF-A Quadrants 19.7 23.38 2.99
SAMURAI Quadrants 22.84 8.61 0.89
NeRD GT 26.88 — —
Neural-PIL GT 27.73 — —

New SAMURAI datasets (No poses recoverable)
Method Pose Init PSNR ↑
BARF-A Quadrants 16.9
SAMURAI Quadrants 23.46

Conclusion

Conclusion

Shape

  • 3D reconstruction from input images
  • Mesh for downstream applications

Appearance

  • Convincing BRDF materials estimation
  • Enables relighting
  • Neural-PIL: General priors guiding the estimation
  • Efficient rendering in downstream applications

Illumination

  • NeRD uses SGs to efficiently integrate illumination
  • Neural-PIL guides the estimation from general priors
  • Varying & fixed illumination possible

Pose

  • SAMURAI does not require GT poses
  • BRDF decomposition is beneficial
  • First to handle full decomposition alongside pose recovery
Conclusion
Method Shape Appearance Light Pose Novel View Relightable Down- stream Varying Light Varying Locations No Masks
NeRD ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌
Neural-PIL ✔ ✔ ✔ ❌ ✔ ✔ ✔ ✔ ❌ ❌
SAMURAI ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✔ ✱
Thanks
  • Nadine and Samuel
  • My parents

  • Hendrik
  • The entire group
  • My office neighbors Raphael and Patrick
  • My collaborators - especially Varun and Jon
  • The committee Andreas Schilling, Gerard Pons-Moll, George Drettakis

Retreat 2021

Publications
SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections
Mark Boss, Andreas Engelhardt, Abhishek Kar, Yuanzhen Li, Deqing Sun, Jonathan T. Barron, Hendrik P. A. Lensch, Varun Jampani - Advances in Neural Information Processing Systems - 2022
Medicine quality screening: TLCyzer, an open-source smartphone-based imaging algorithm for quantitative evaluation of thin-layer chromatographic analyses using the GPHF Minilab
Cathrin Hauk, Mark Boss, Julia Gabel, Simon Schäfermann, Hendrik P. A. Lensch, Lutz Heide - Scientific Reports - 2022
Neural-PIL: Neural Pre-Integrated Lighting for Reflectance Decomposition
Mark Boss, Varun Jampani, Raphael Braun, Ce Liu, Jonathan T. Barron, Hendrik P. A. Lensch - Advances in Neural Information Processing Systems - 2021
NeRD: Neural Reflectance Decomposition from Image Collections
Mark Boss, Raphael Braun, Varun Jampani, Jonathan T. Barron, Ce Liu, Hendrik P. A. Lensch - IEEE International Conference on Computer Vision - 2021
Two-shot Spatially-varying BRDF and Shape Estimation
Mark Boss, Varun Jampani, Kihwan Kim, Hendrik P. A. Lensch, Jan Kautz - IEEE Conference on Computer Vision and Pattern Recognition - 2020
Single Image BRDF Parameter Estimation with a Conditional Adversarial Network
Mark Boss, Hendrik P. A. Lensch - ArXiv - 2019
Deep Dual Loss BRDF Parameter Estimation
Mark Boss, Fabian Groh, Sebastian Herholz, Hendrik P. A. Lensch - Workshop on Material Appearance Modeling - 2018
Invisible

Thank you for listening