Inverse Rendering for Games
Presented By
Mark Boss
Senior Research Scientist
Biography
Profile
Mark Boss is a researcher at Unity Technologies. Before that, he completed his PhD at the University of Tübingen in the computer graphics group of Prof. Hendrik Lensch. His research interests lie at the intersection of machine learning and computer graphics, with the main focus on inferring physical properties (shape, material, illumination) from images.
Experience
Senior Research Scientist
Unity
Sep 2022 - present
Student Researcher
June 2021 - April 2022
Research Intern
Nvidia
April 2019 - Juli 2019
Ph.D. Student
University of Tübingen
June 2018 - Juli 2022
What is Inverse Rendering?
Multiple input images (potential multiple illuminations)
Relightable 3D asset [1]
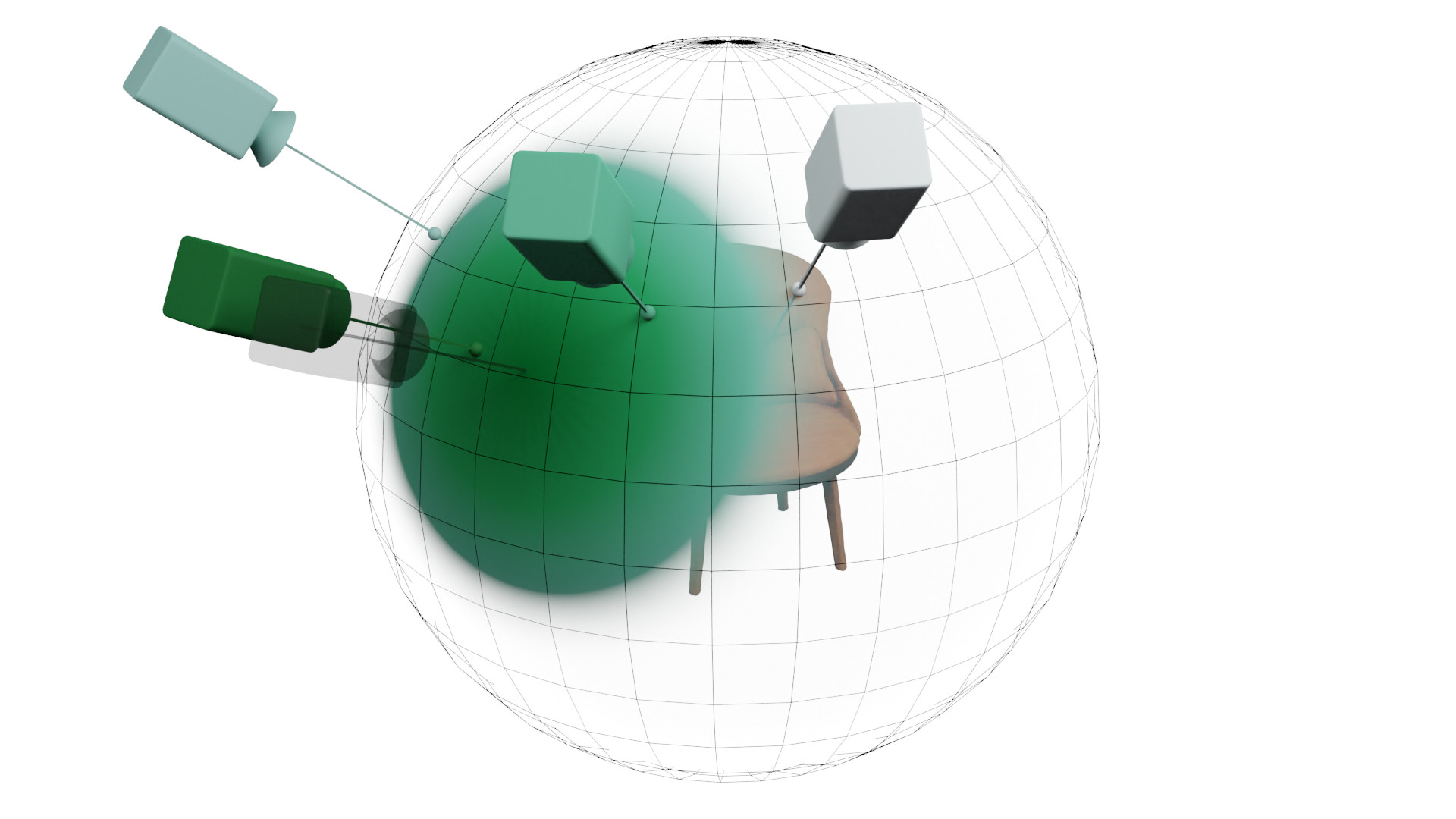
[1] Result from: Boss et al. - NeRD: Neural Reflectance Decomposition from Image Collections - 2021
Why Inverse Rendering?
Far Cry 4 (2014)
The Last Of Us - Left Behind (2014)
Shadow of Mordor (2014)
Vanishing of Ethan Carter (2014)
Indie Team < 10 people
Photogrammetry in Vanishing of Ethan Carter
Scanning in the field
Reconstruction in Software
[1] Images from: The Astronauts - Blog
Speedup In Asset Creation
| Days | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Classic | High Mesh | Texturing | Retopology | UV + bake | Material | Import IG | LOD | |||||||
| Photogrammetry | Photos | HM + T | Retopology | UV + bake | Material & Delight | Import IG | LOD | Time saved | ||||||
[1] Create Photorealistic Game Assets - E-Book - Unity Technologies - 2017
Issues with Photogrammetry
- Requires De-lighting
- Requires manual material creation
- Manual material creation is time consuming
- Manual material creation also does not necessarily capture the reality
Delighting [1]
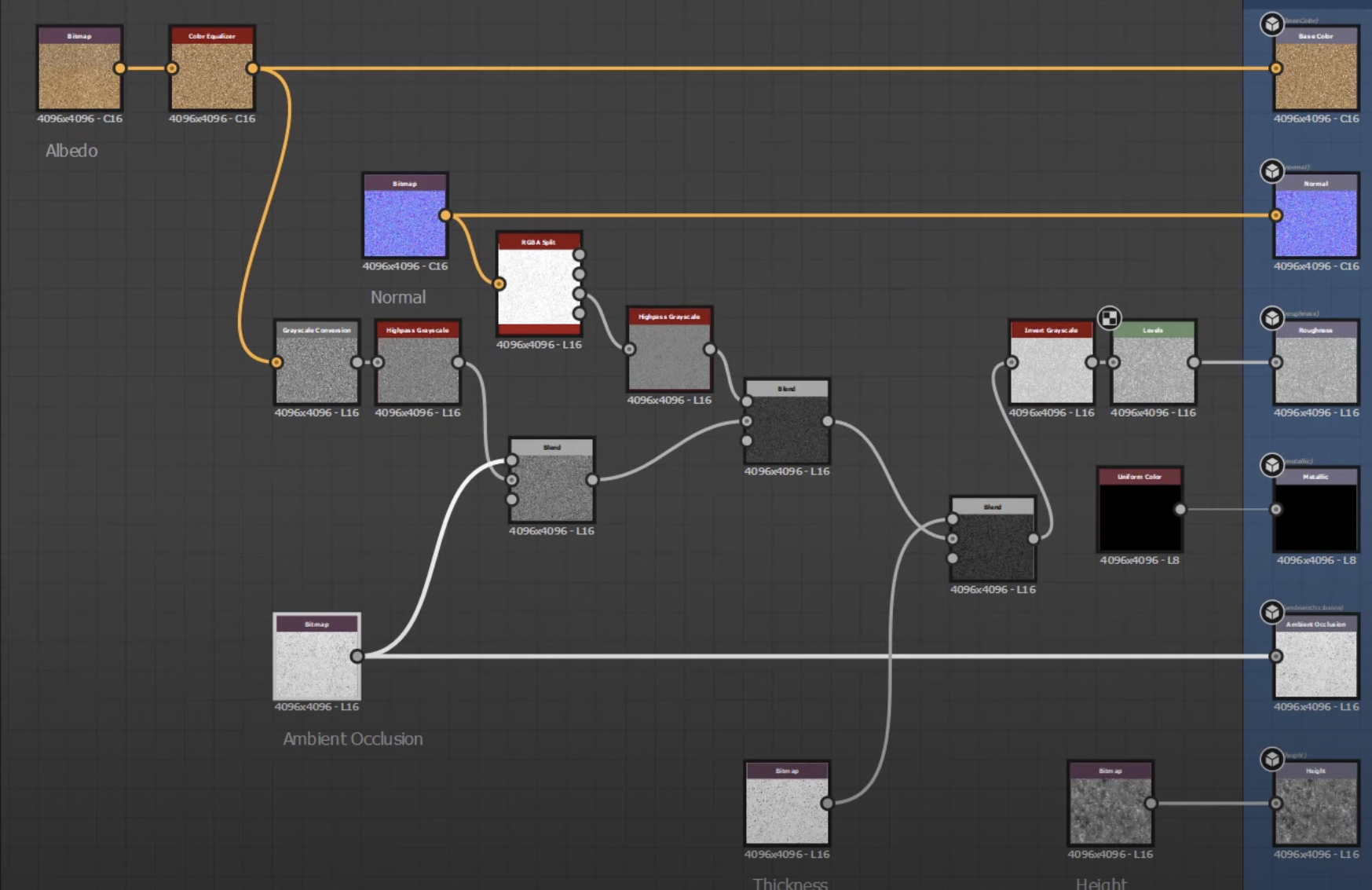
Material Creation in Substance Designer [2]
[1] Create Photorealistic Game Assets - E-Book - Unity Technologies - 2017
[2] Photogrammetry workflow for surface scanning with the monopod - Grzegorz Baran - 2020
Speedup In Asset Creation
| Days | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Classic | High Mesh | Texturing | Retopology | UV + bake | Material | Import IG | LOD | |||||||
| Photogrammetry | Photos | HM + T | Retopology | UV + bake | Material & Delight | Import IG | LOD | Time saved | ||||||
| Neural Decomposition | Photos | HM + T + M | Retopology | UV + bake | Import IG | LOD | Time saved | |||||||
[1] Create Photorealistic Game Assets - E-Book - Unity Technologies - 2017
Background
Rendering
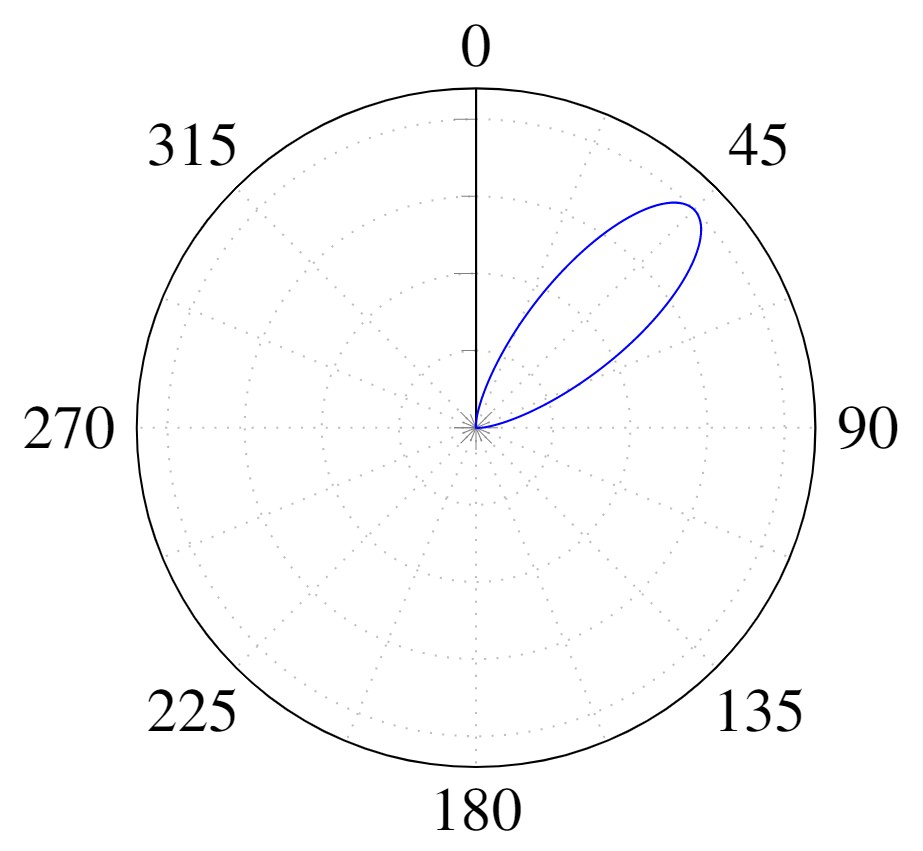
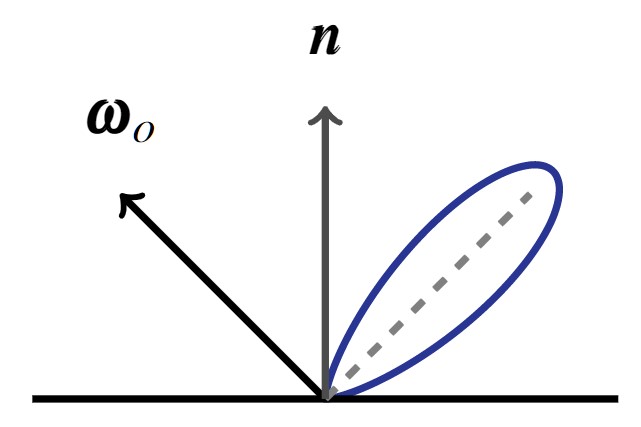
[1] James T. Kajiya - The Rendering Equation - 1986
Rendering equation [1]
$$ \definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,= \fragment{1}{\,\color{emit}L_{e}({\mathbf x},\,\omega_{o})} \fragment{2}{\color{black} + \\ \color{int}\int_{\Omega }} \fragment{4}{\color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o})} \fragment{3}{\color{in}L_{i}({\mathbf x},\,\omega_{i})}\, \fragment{5}{\color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})}\, \fragment{2}{\color{int}\operatorname d\omega_{i}}$$
Simplification: No self-emittance
$$ \definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,=\,\color{int}\int_{\Omega} \color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) \color{in}L_{i}({\mathbf x},\,\omega_{i})\, \color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})\, \color{int}\operatorname d\omega_{i}$$
Radiance, reflectance and irradiance
$$\underbrace{L_{o}({\mathbf x},\,\omega_{o})}_{\text{Radiance (Outgoing)}}\,=\,\int_{\Omega}\underbrace{f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o})}_{\text{Reflectance}} \\ \underbrace{L_{i}({\mathbf x},\,\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}}_{\text{Irradiance}}$$
Infinitely Far Illumination
$$ \definecolor{point}{RGB}{232,0,19} L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\color{point}{\mathbf x}\color{black},\,\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$
Simplification: Illumination only dependent on direction
$$L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$
Bidirectional Reflectance Distribution Function
Inverse Rendering - Workshop Metaphor [1]
Image
Sculptor
Painter
Gaffer
Possible explanation
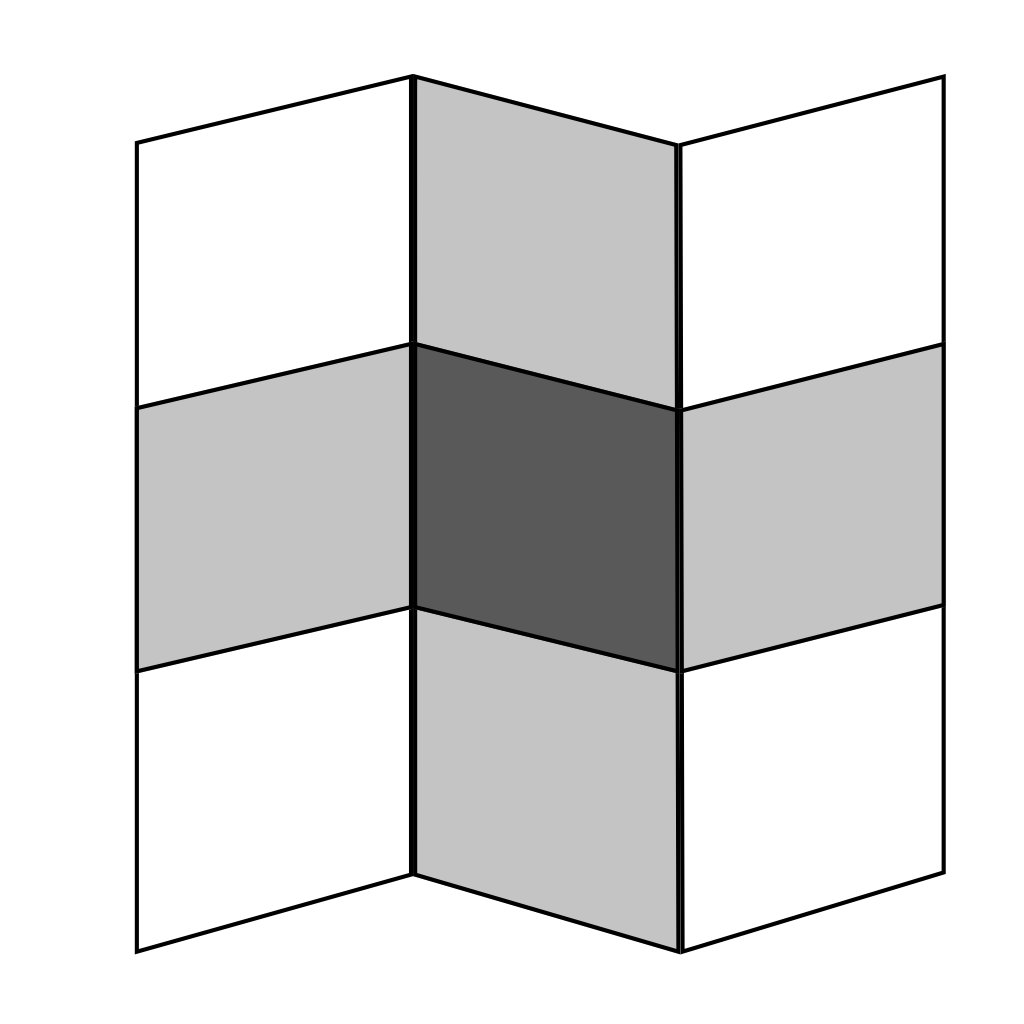
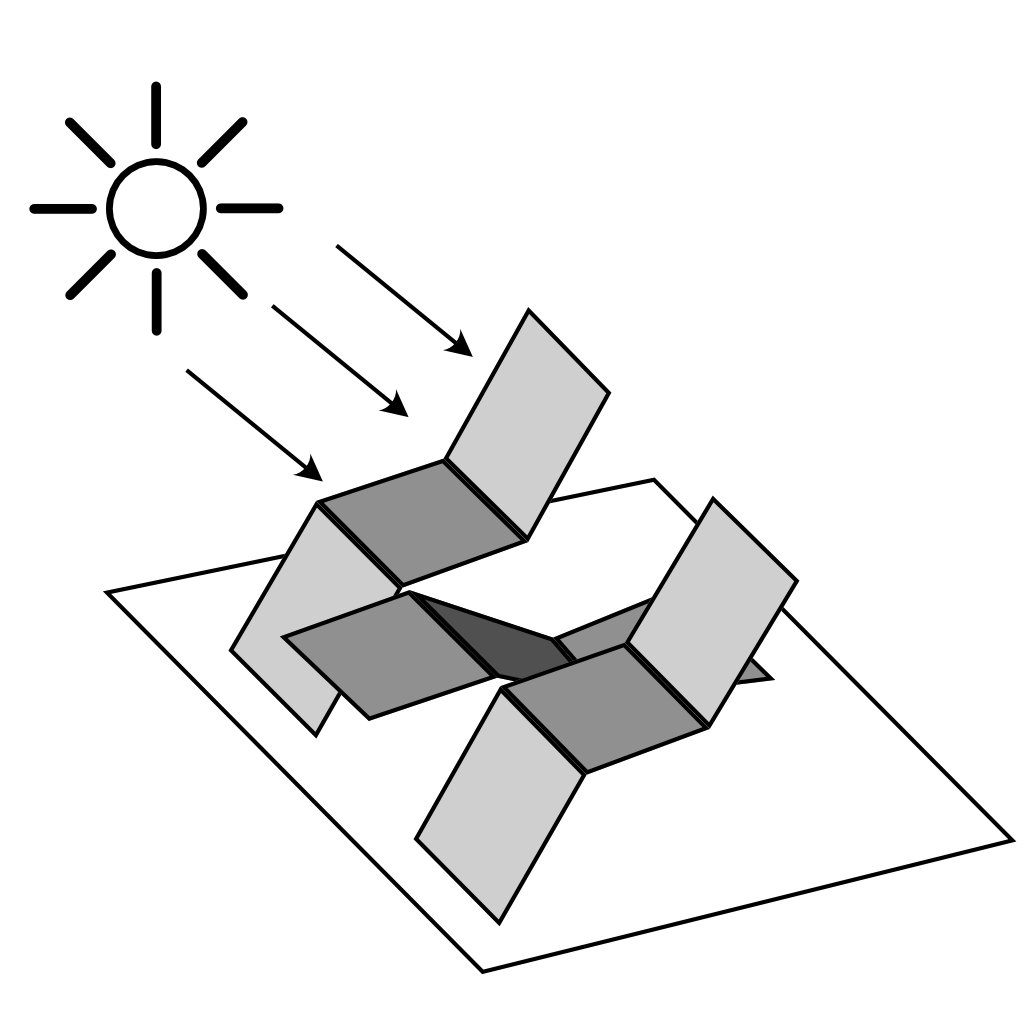
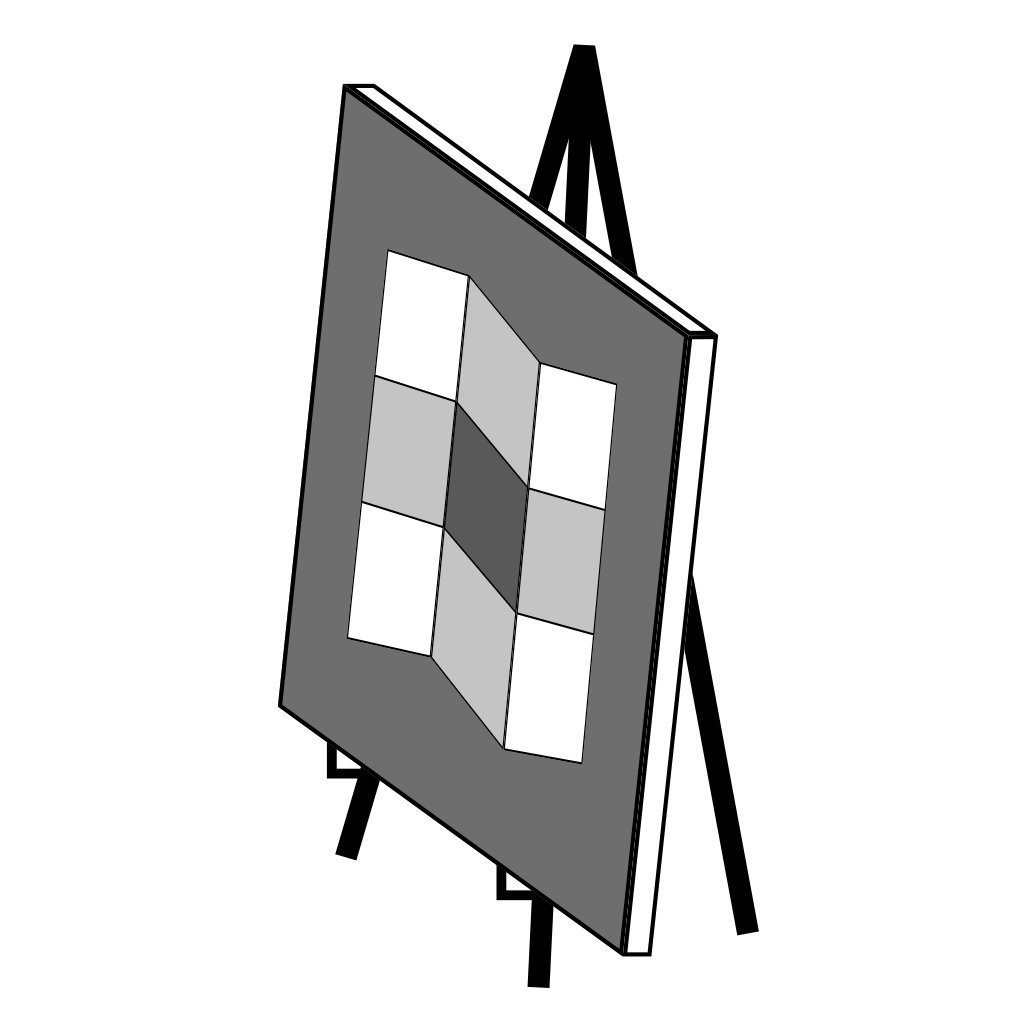
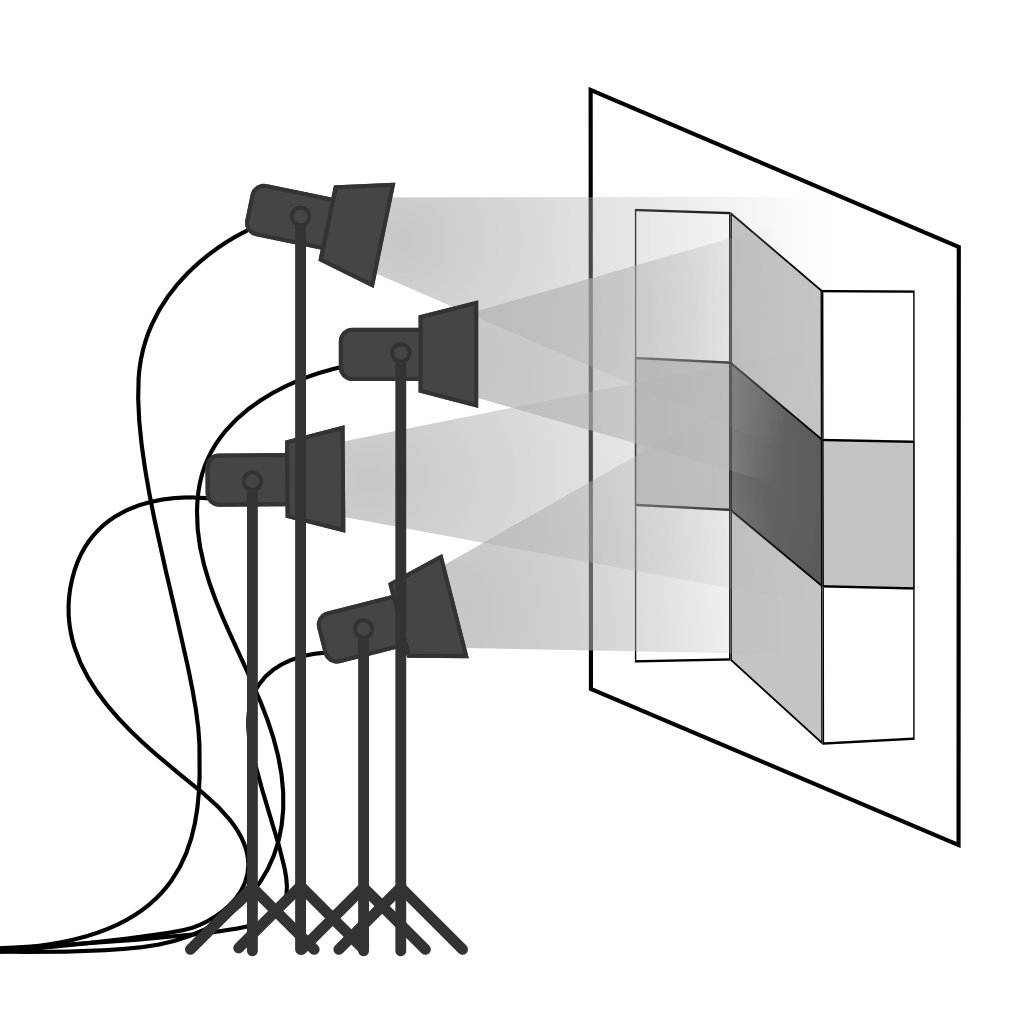
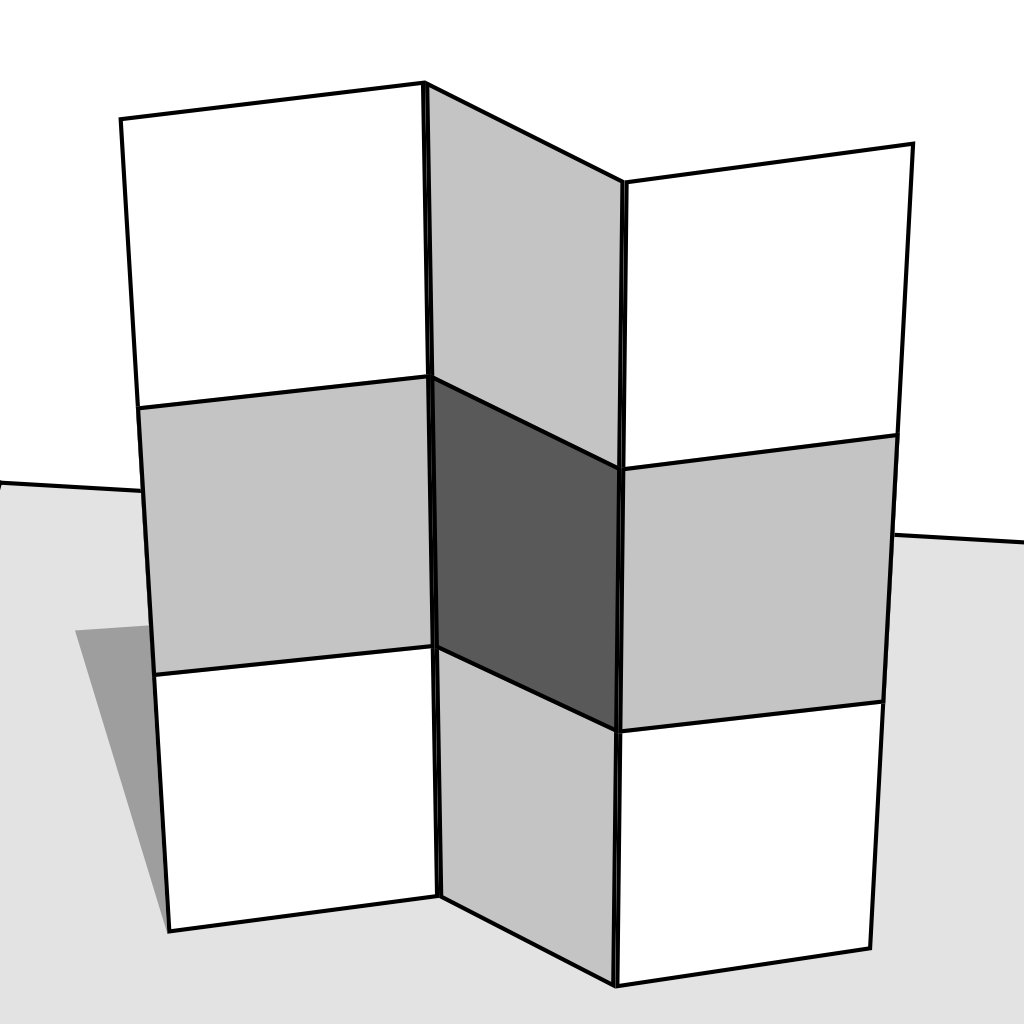
[1] E.H. Adelson, A.P. Pentland - The Perception of Shading and Reflectance - 1996
Preliminaries - NeRF
NeRF: Neural Radiance Fields
- NeRF [1] is a method for photorealistic results in novel view synthesis
- Goal is to create a 3D radiance field from multiple images
- Images have known poses
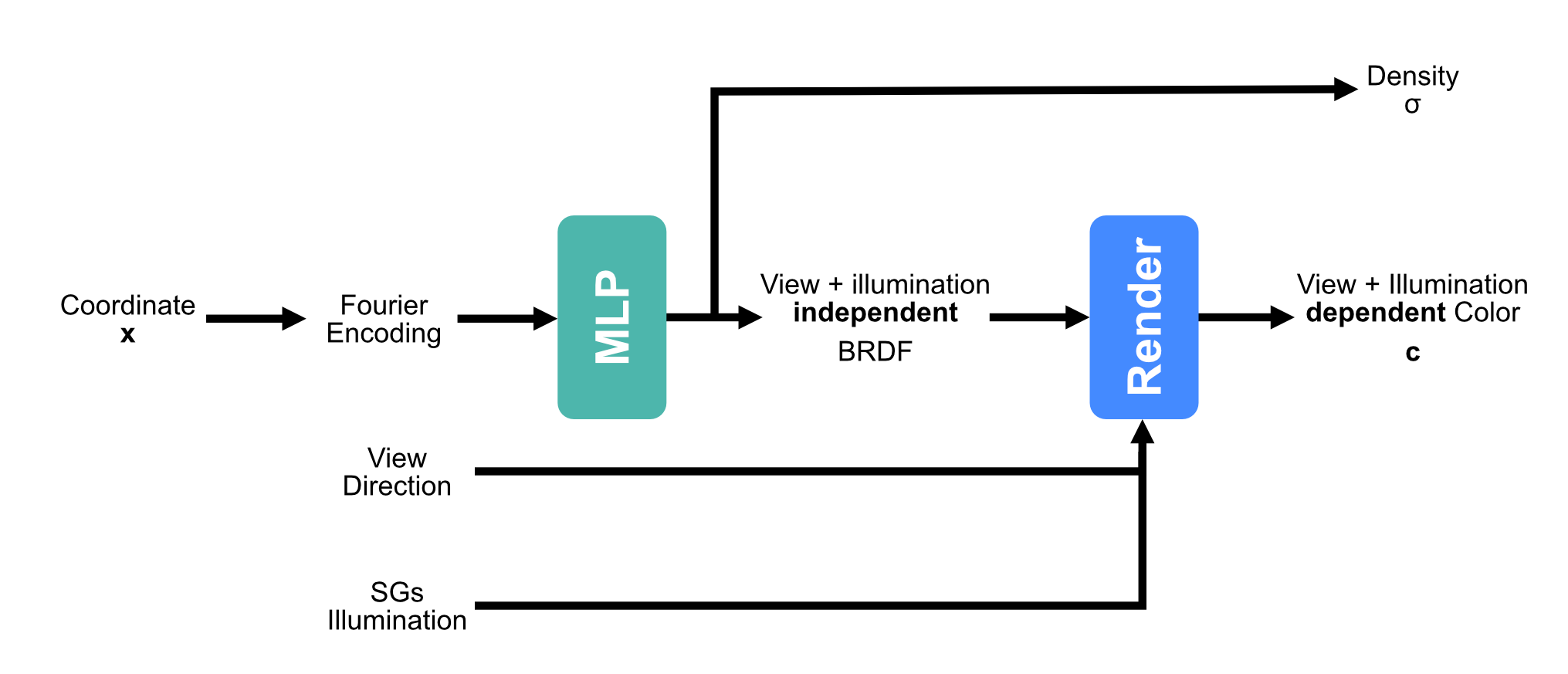
[1] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020
NeRF - Visualization
NeRF - Architecture
- Main section of NeRF learns density and latent code
- Last layers of NeRF estimates view-dependent color
- Shape should not be influenced by the viewing direction
- NeRF is not relightable
View dependence with NeRF
NeRF architecture
Fourier encoding
- Sinusoidal embedding with increasing frequencies
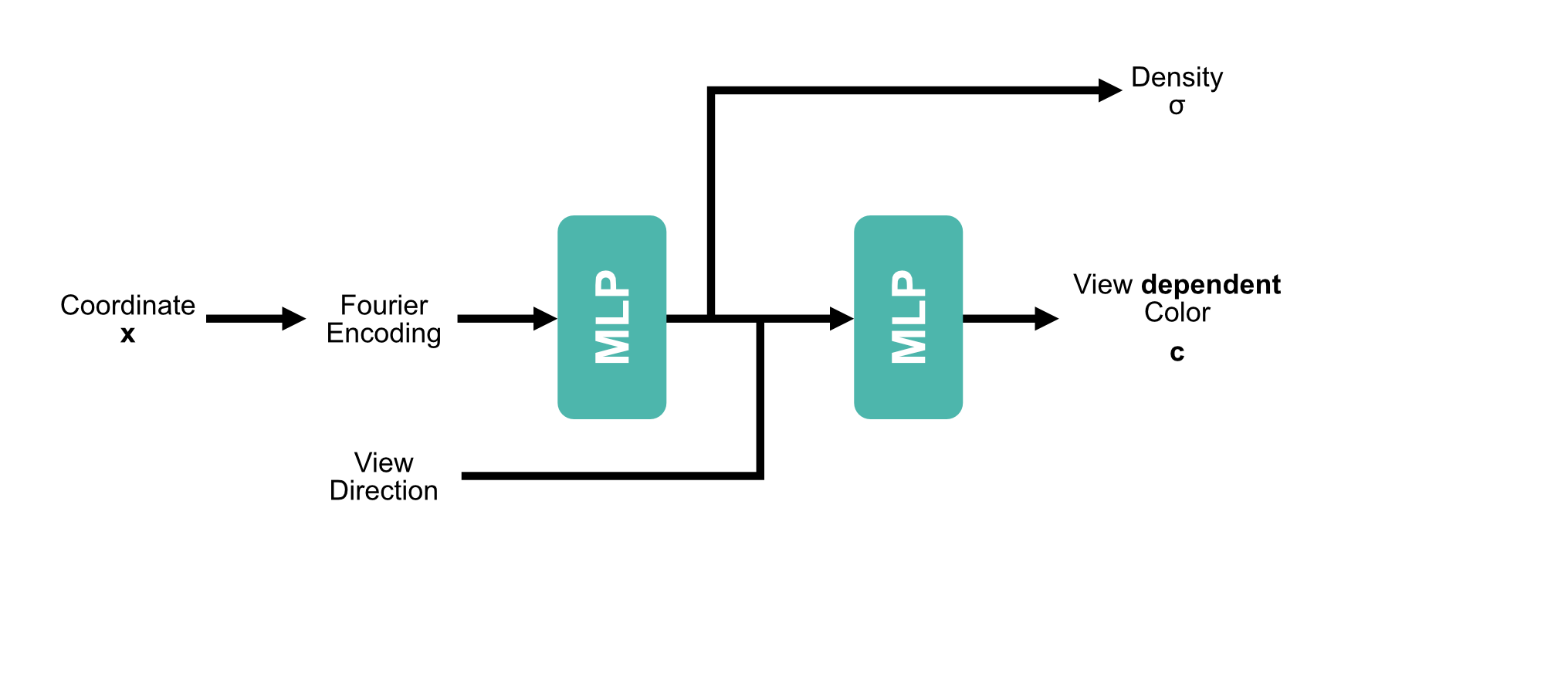
$$\gamma(x) = (\sin(2^l x))^{L-1}_{l=0}$$
Methods
NeRD: Neural Reflectance Decomposition from Image Collections
Mark Boss, Raphael Braun, Varun Jampani, Jonathan T. Barron, Ce Liu, Hendrik P. A. Lensch
IEEE International Conference on Computer Vision 2021
IEEE International Conference on Computer Vision 2021
Amplifying NeRF for Full Relighting
NeRF architecture
NeRF-A architecture
NeRD architecture
Spherical Gaussians
Rendering equation
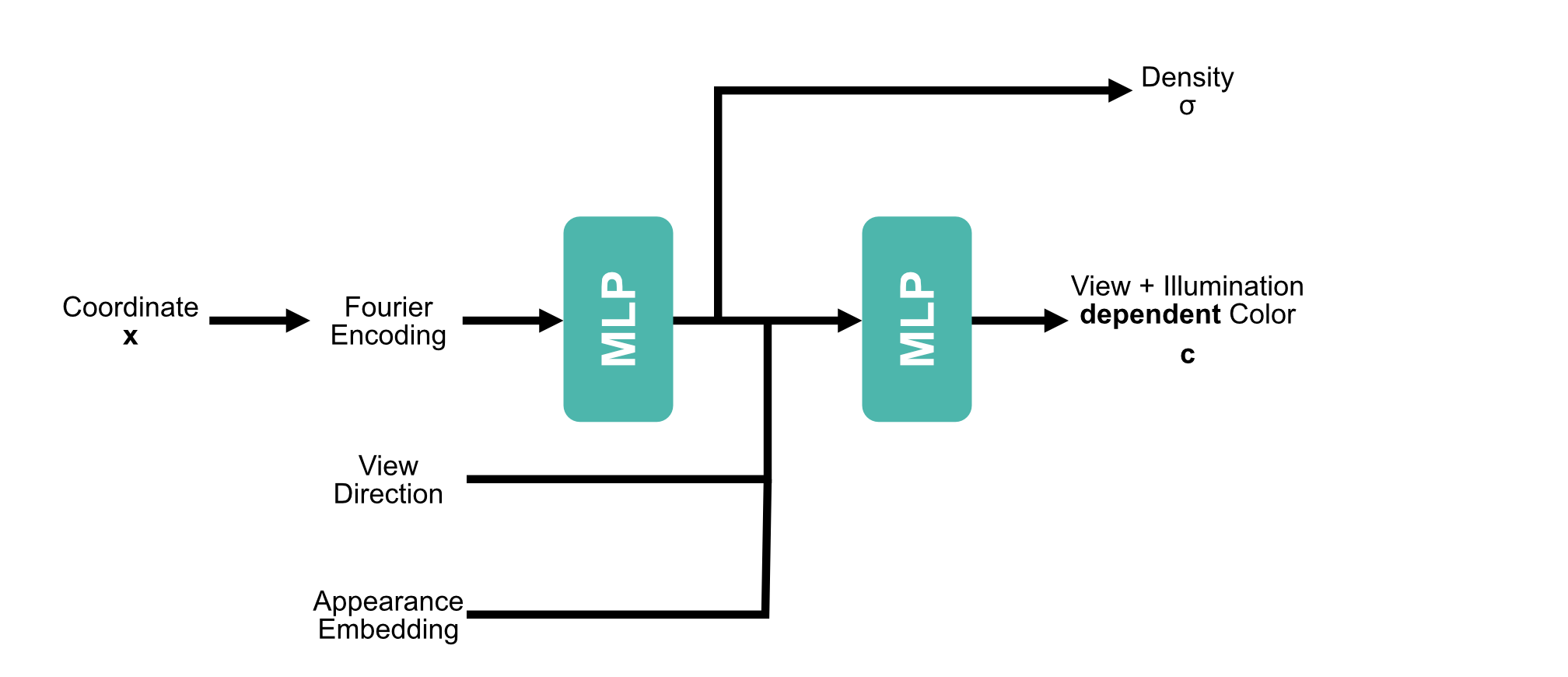
$$L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$$
- Rendering requires integrating all incoming light
- Spherical Gaussian (SG) have convenient properties
- Close-form solution exists for integration 2 SGs
- Product of 2 SGs is a SG
- Represent illumination and BRDF as SGs
- Closed form integration enables fast rendering
- No sampling noise compared to Monte Carlo integration
Downstream: Mesh Extraction
- Extracting textured meshes allows multiple use cases
Results
Comparisons - Single Illumination
Input
Comparisons - Single Illumination
GT
NeRF
NeRD
Results - Novel View Synthesis
| Method | Single | Multiple |
|---|---|---|
| NeRF | 34.24 | 21.05 |
| NeRF-A | 32.44 | 28.53 |
| NeRD (Ours) | 30.07 | 27.96 |
| Method | Single | Multiple |
|---|---|---|
| NeRF | 23.34 | 20.11 |
| NeRF-A | 22.87 | 26.36 |
| NeRD (Ours) | 23.86 | 25.81 |
SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections
Mark Boss, Andreas Engelhardt, Abhishek Kar, Yuanzhen Li, Deqing Sun, Jonathan T. Barron,
Hendrik P. A. Lensch, Varun Jampani
Advances in Neural Information Processing Systems 2022
Advances in Neural Information Processing Systems 2022
Traditional Pose Recovery Fails
Main Idea
- Move previous methods to real-world online collections
- Traditional pose estimation failed on these datasets
- No features can be used in backgrounds and foreground vary too much
Decomposition from Coarsely Posed Images
Coarse-to-Fine & Camera Multiplex
- Fourier Encoding Annealing from BARF [1]
- Increases encoding frequencies during training
- Higher $L$ are blended in
- Smooth shapes easier to align
Positional encoding
$$\gamma(x) = (\sin(2^l x))^{L-1}_{l=0}$$
- Gradual increase in resolution
- Multiple camera estimates
- Posterior scaling only allows best camera to optimize volume
Coarse-to-fine during training
[1] Lin et al. - BARF: Bundle-adjusting neural radiance fields
Camera Multiplex
Image Posterior Scaling
- Posterior scaling also applied on image level
- Influence of badly aligned images or segmentation masks reduced
- Scaling based on running average of losses
Influence of poorly aligned images is reduced
Results
Results
Comparison with BARF
Exemplary Inputs
BARF
SAMURAI
NeRF View Conditioning
NeRF architecture
Frozen position with view conditioning
BARF Conditioning Entanglement
Moving Camera
BARF
SAMURAI
View Conditioning
Results - Novel View Synthesis
| Method | Pose Init | PSNR ↑ | Translation Error ↓ | Rotation° Error ↓ |
|---|---|---|---|---|
| BARF [1] | Quadrants | 14.96 | 34.64 | 0.86 |
| GNeRF [2] | Random | 20.3 | 81.22 | 2.39 |
| NeRS [3] | Quadrants | 12.84 | 32.77 | 0.77 |
| SAMURAI | Quadrants | 21.08 | 33.95 | 0.71 |
| NeRD | GT | 23.86 | — | — |
| Neural-PIL | GT | 23.95 | — | — |
[1] Lin et al. - BARF: Bundle-adjusting neural radiance fields
[2] Meng et al. - GNeRF: GAN-based Neural Radiance Field without Posed Camera
[3] Zhang et al. - NeRS: Neural reflectance surfaces for sparse-view 3d reconstruction in the wild
Results - Novel View Synthesis & Relighting
| Method | Pose Init | PSNR ↑ | Translation Error ↓ | Rotation° Error ↓ |
|---|---|---|---|---|
| BARF-A | Quadrants | 19.7 | 23.38 | 2.99 |
| SAMURAI | Quadrants | 22.84 | 8.61 | 0.89 |
| NeRD | GT | 26.88 | — | — |
| Neural-PIL | GT | 27.73 | — | — |
| Method | Pose Init | PSNR ↑ |
|---|---|---|
| BARF-A | Quadrants | 16.9 |
| SAMURAI | Quadrants | 23.46 |
Conclusion
Conclusion
Shape
- 3D reconstruction from input images
- Mesh for downstream applications
Appearance
- Convincing BRDF materials estimation
- Enables relighting
- Efficient rendering in downstream applications
Illumination
- Environment estimation from unconstrained data
- NeRD uses SGs to efficiently integrate illumination
- Varying & fixed illumination possible
Pose
- SAMURAI does not require GT poses
- Can run where traditional pose recovery fails
- BRDF decomposition is beneficial
- First to handle full decomposition alongside pose recovery
Are we there yet?
- No, but we are getting closer
Mesh extraction
- Meshes are still the most common downstream representation
- Models are volumetric
- Volumetric models are easier to optimize
- Marching Cubes most commonly used, but meshes do not look good
- FlexiCubes [1] is a recent approach which improves upon this
General Decomposition Improvements
- BRDF, illumination, and shape work in conjunction
- An improvement in one area leads to improvement in others
- Currently, far-field illumination is often used, but near-field illumination is more realistic
- Global illumination is highly important for large scenes
- Shadowing is important for appearance and shape
- High-frequent illumination is important for appearance (reflections)
[1] Shen et al. - Flexible Isosurface Extraction for Gradient-Based Mesh Optimization - 2023
Current works
- 3D Gaussian Splatting [1]
- Instead of learning a 3D volume, the scene optimizes a variable number of 3D Gaussians
- Splatting is quite popular in graphics and proven fast in demoscene projects
- Rendering changes: Instead of rendering each pixel with many samples individually, primitives are rendered instead.
- For example: Full HD with 128 samples equals: 1920x1080x128 = 265,420,800 samples
Interactive Demos
[1] Kerbl et al. - 3D Gaussian Splatting for Real-Time Radiance Field Rendering - 2023
Invisible