Interview Presentation

Multiple input images (potential multiple illuminations)

Relightable 3D asset [1]

[1] Result from: Boss et al. - NeRD: Neural Reflectance Decomposition from Image Collections - 2021

Boss et al. - SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections - 2022

[1] James T. Kajiya - The Rendering Equation - 1986

Rendering equation [1]

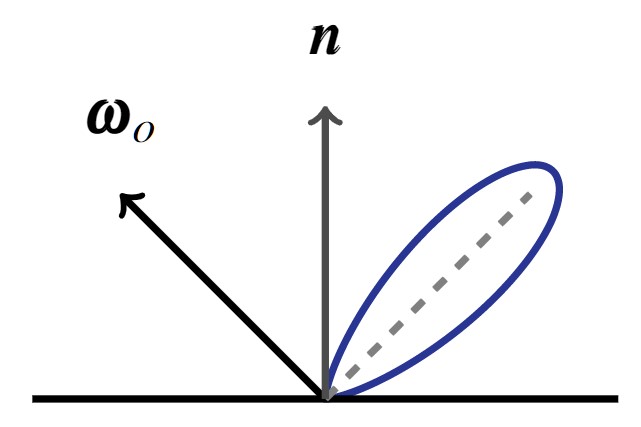
$\definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,= \fragment{1}{\,\color{emit}L_{e}({\mathbf x},\,\omega_{o})} \fragment{2}{\color{black} + \\ \color{int}\int_{\Omega }} \fragment{4}{\color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o})} \fragment{3}{\color{in}L_{i}({\mathbf x},\,\omega_{i})}\, \fragment{5}{\color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})}\, \fragment{2}{\color{int}\operatorname d\omega_{i}}$

Simplification: No self-emittance

$\definecolor{out}{RGB}{219,135,217} \definecolor{emit}{RGB}{125,194,103} \definecolor{int}{RGB}{127,151,236} \definecolor{in}{RGB}{225,145,83} \definecolor{brdf}{RGB}{0,202,207} \definecolor{ndl}{RGB}{235,120,152} \definecolor{point}{RGB}{232,0,19} \color{out}L_{o}(\color{point}{\mathbf x}\color{out},\,\omega_{o})\color{black}\,=\,\color{int}\int_{\Omega} \color{brdf}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) \color{in}L_{i}({\mathbf x},\,\omega_{i})\, \color{ndl}(\omega_{i}\,\cdot\,{\mathbf n})\, \color{int}\operatorname d\omega_{i}$

Radiance, reflectance and irradiance

$\underbrace{L_{o}({\mathbf x},\,\omega_{o})}_{\text{Radiance (Outgoing)}}\,=\,\int_{\Omega}\underbrace{f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o})}_{\text{Reflectance}} \\ \underbrace{L_{i}({\mathbf x},\,\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}}_{\text{Irradiance}}$

$\definecolor{point}{RGB}{232,0,19} L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\color{point}{\mathbf x}\color{black},\,\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$

Simplification: Illumination only dependent on direction

$L_{o}({\mathbf x},\,\omega_{o})\,=\,\int_{\Omega}f_{r}({\mathbf x},\,\omega_{i},\,\omega_{o}) L_{i}(\omega_{i})\, (\omega_{i}\,\cdot\,{\mathbf n})\, \operatorname d\omega_{i}$

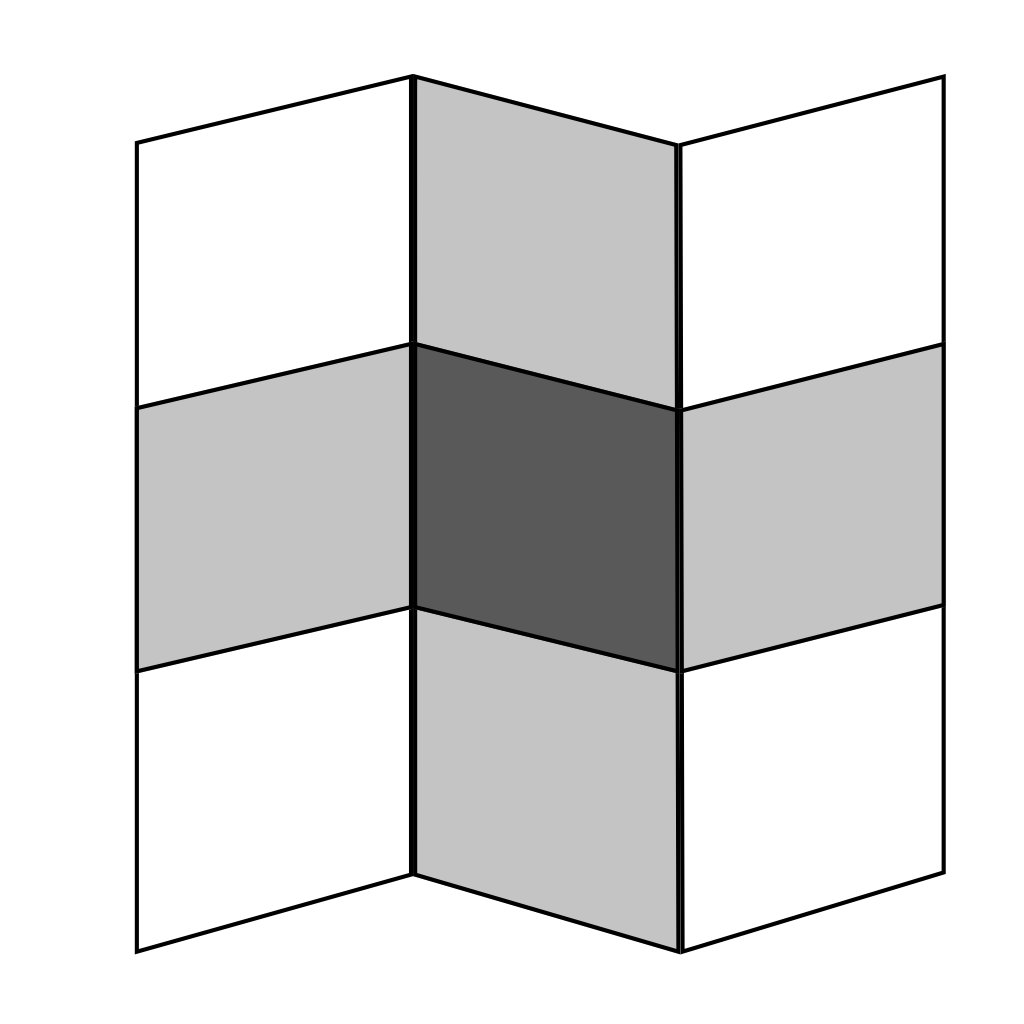
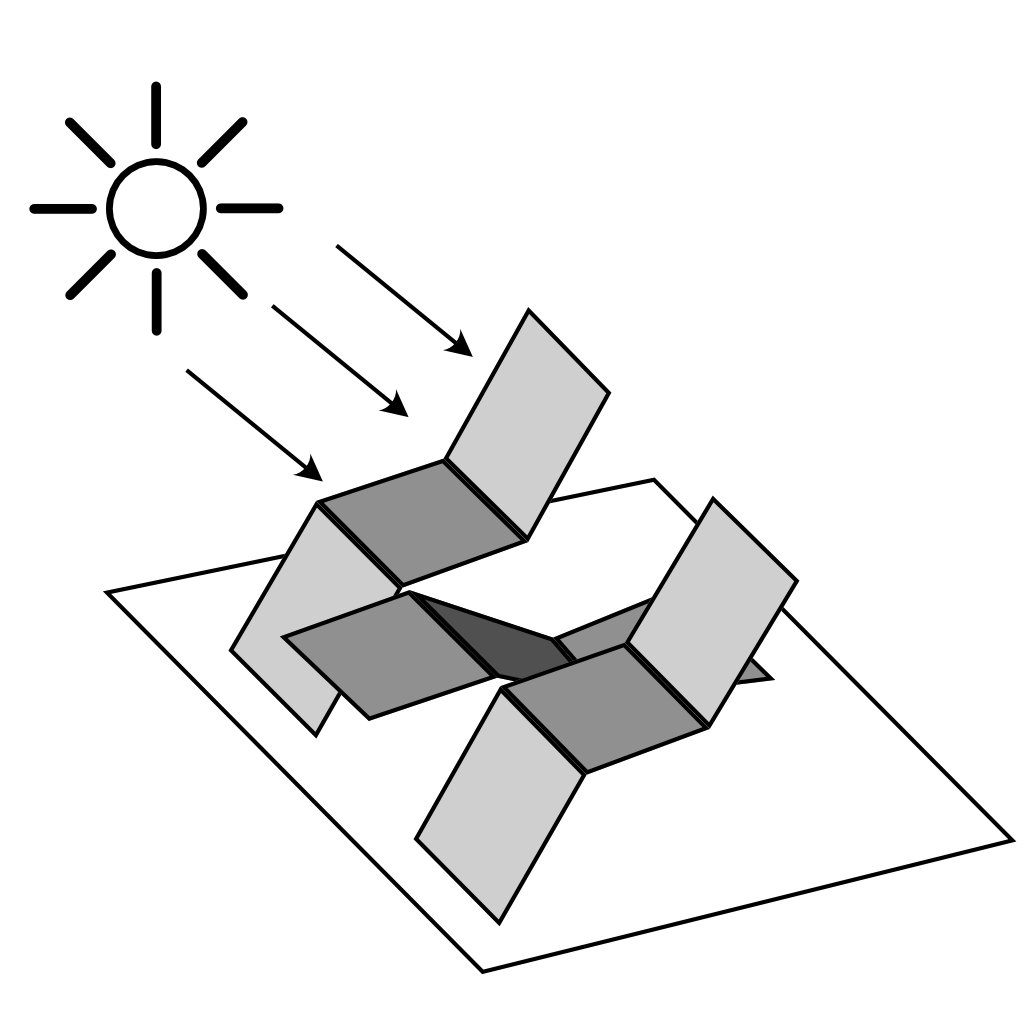
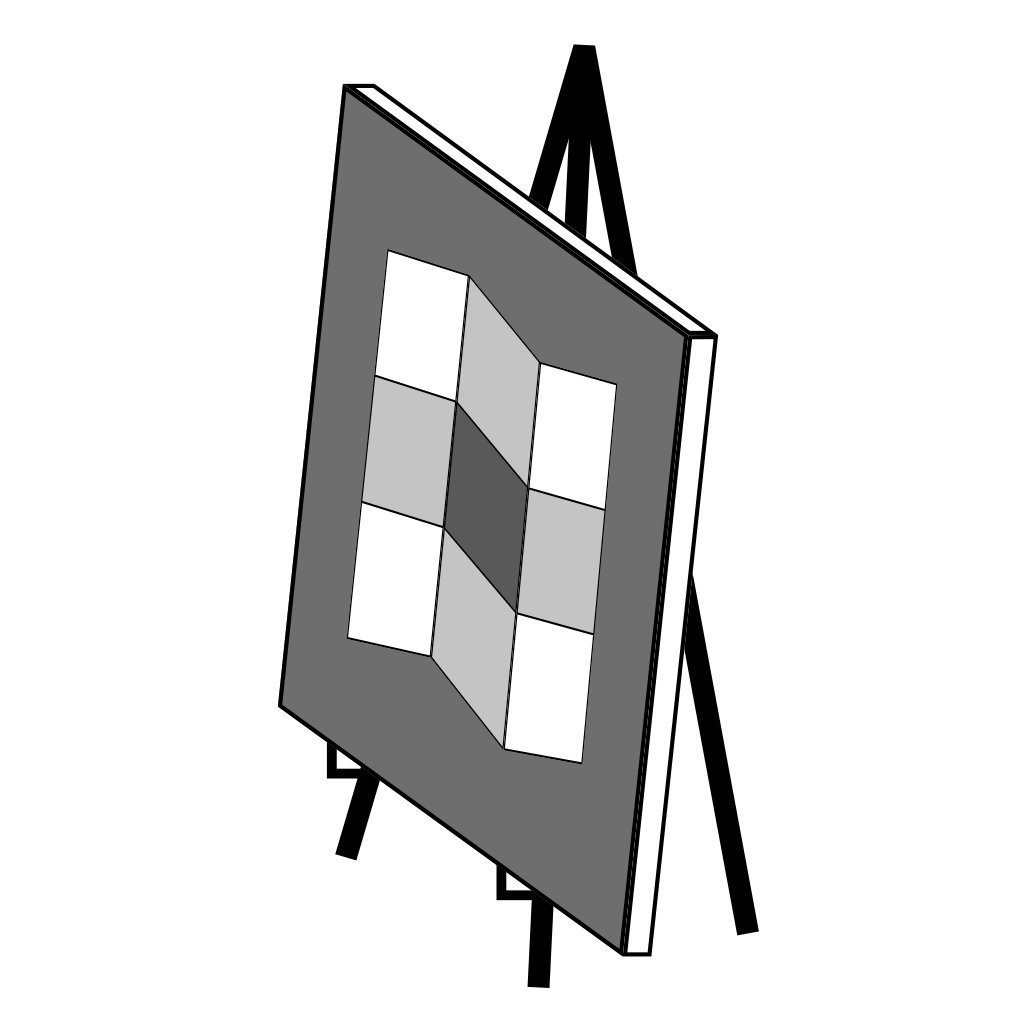
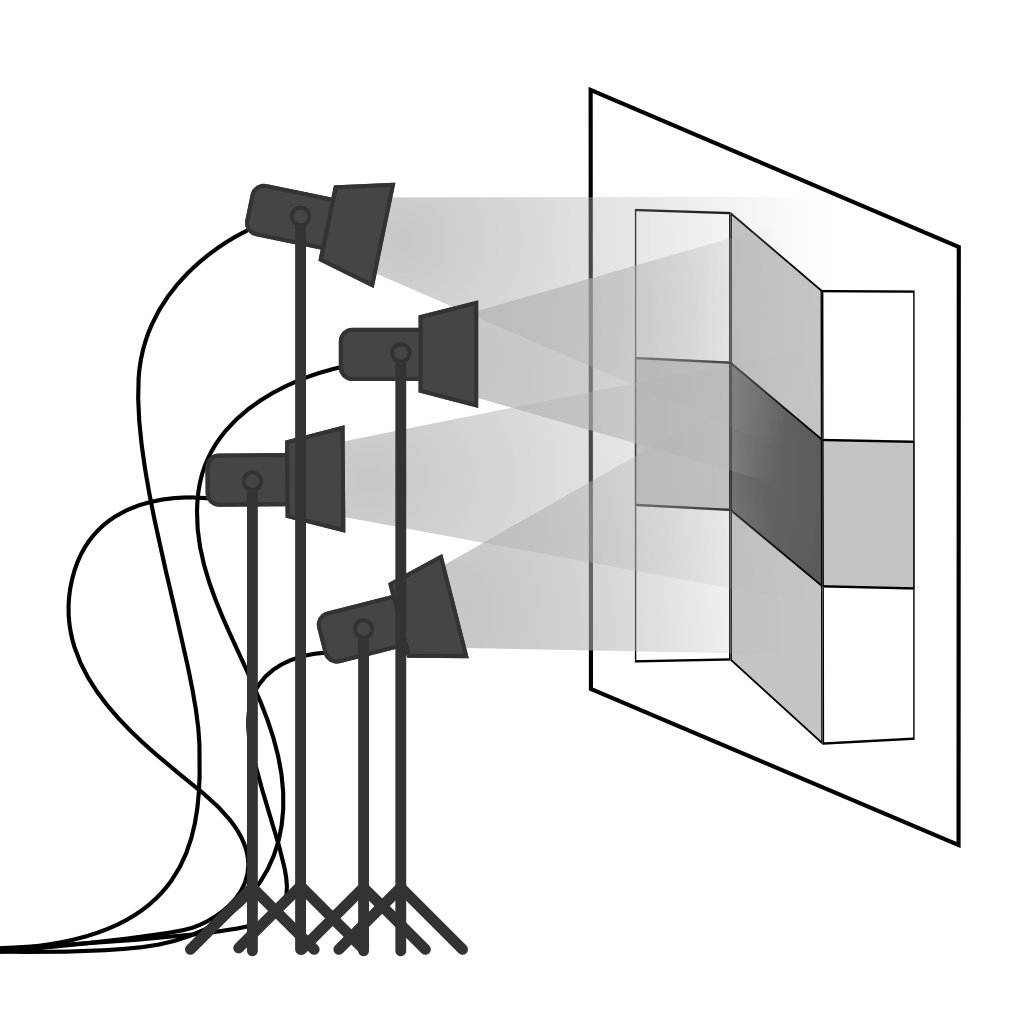
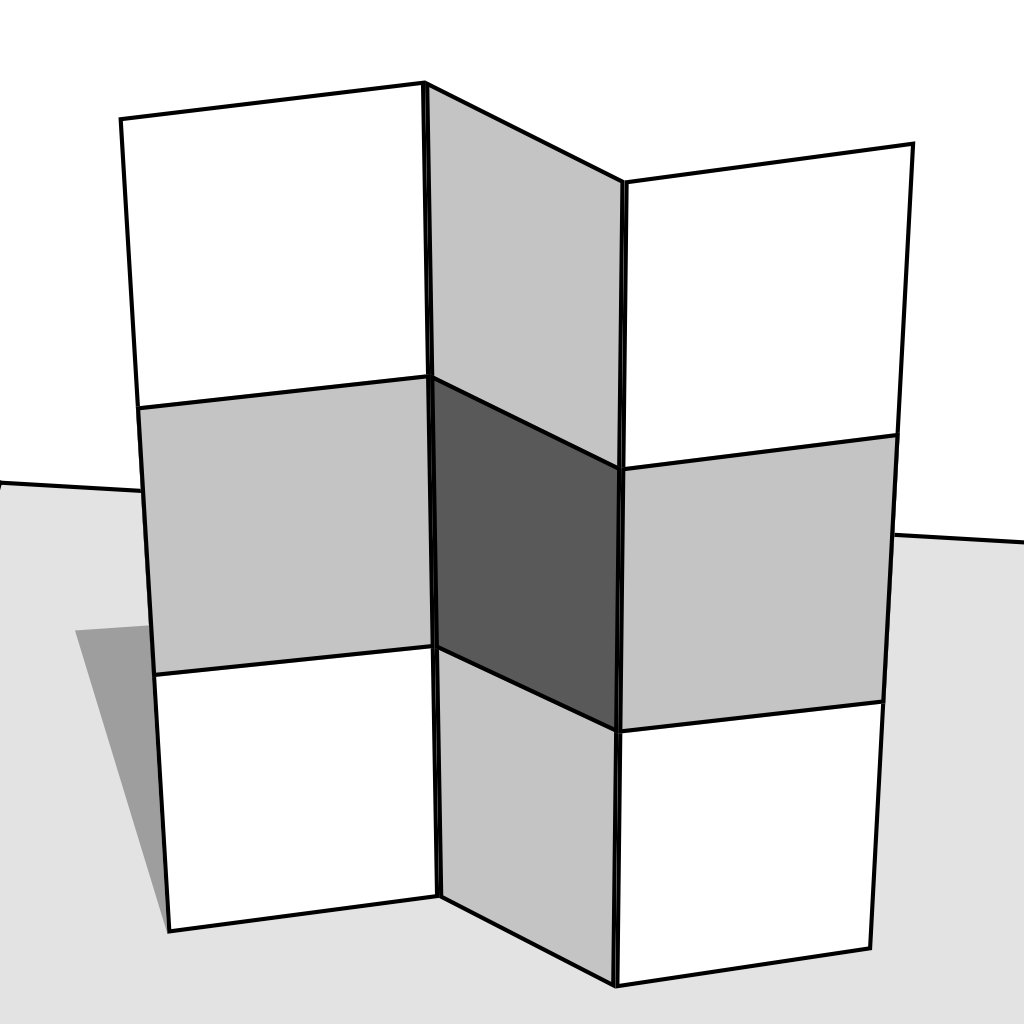
[1] E.H. Adelson, A.P. Pentland - The Perception of Shading and Reflectance - 1996

Plenoptic function

Main use-case: novel view synthesis
Learns the radiance
No relighting possible

Intrinsic image

Splits an image into layers:
- Shading (Irradiance)
- Diffuse albedo
- Potential: Specular shading + albedo
Partial decomposition of the rendering equation
Albedos are accurate up to a shift and scale

Full decomposition

Decomposes the rendering equation
Reflectance modelled as BRDF
- Often analytical
Illumination as incoming radiance
Often differentiable rendering is used for optimization

Assume dataset of 4 images
Images are varying illumination

Potential solution

Train GLO (Generative Latent Optimization) to express radiance per illumination
Interpolate between illuminations

Only interpolate between seen illuminations
No issue if dataset is vast and contains most illuminations
However, it is hard to get all possible illumination edge cases

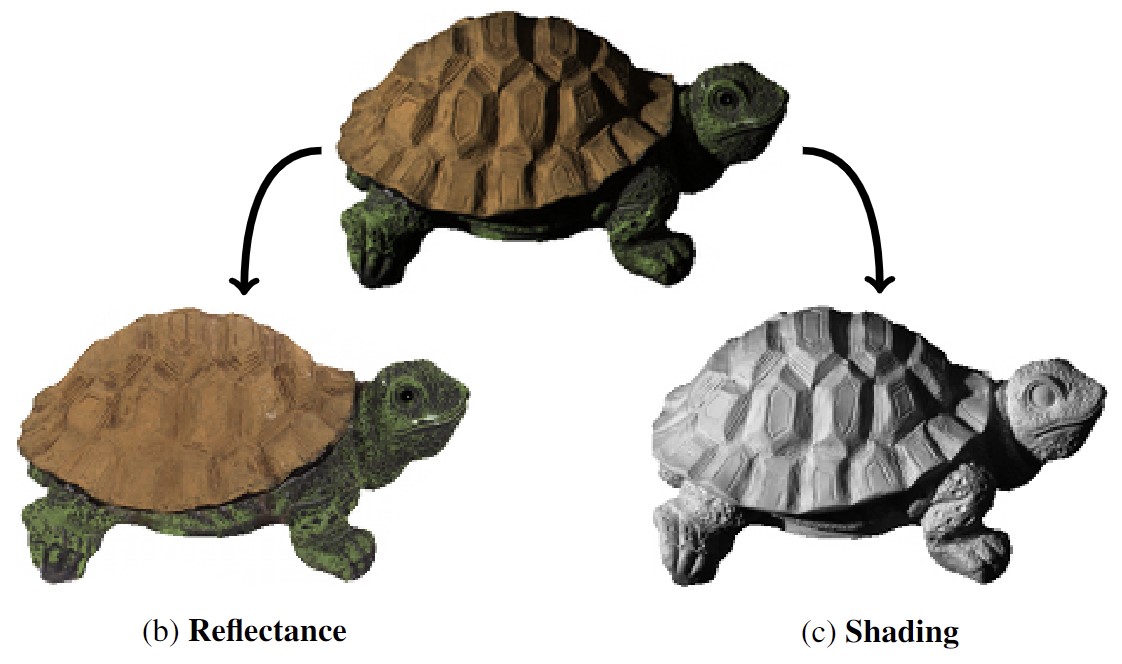
[1] Boss et al. - NeRD: Neural Reflectance Decomposition from Image Collections - 2021

Temporarily also known as: Coordinate-based MLPs
Early works encode points p∈R3 in network as
- Occupancy [1, 2]: $f(p) \rightarrow o; o \in {0, 1}$
- Signed Distance Field [3]: $f(p) \rightarrow d; d \in \mathbb{R}$
Only encode existing point clouds or models in the neural field

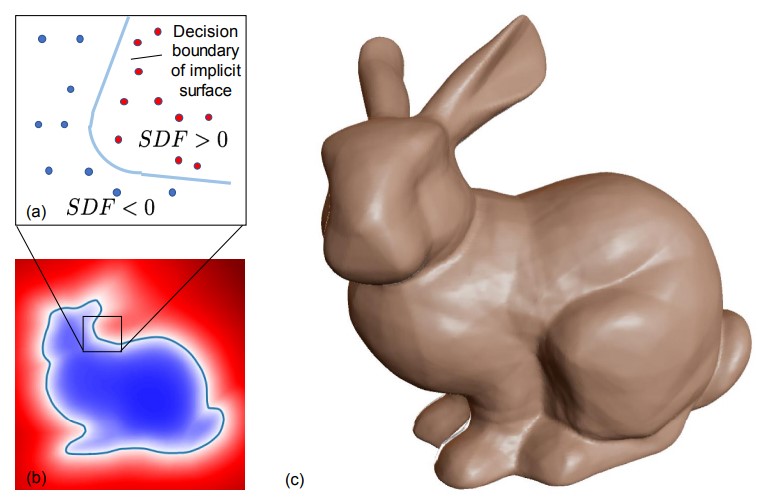
[1] Chen et al. - Learning Implicit Fields for Generative Shape Modeling - 2019

[2] Mescheder et al. - Occupancy Networks: Learning 3D Reconstruction in Function Space - 2019

[3] Park et al. - DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation - 2019

Neural volumetric rendering first introduced by Lombardi et al. [1]
- Accumulate opacity along a ray based on volume rendering

NeRF combined neural fields with volume rendering [2]
Achieved photorealistic results in novel view synthesis

Result from NeRF[2]

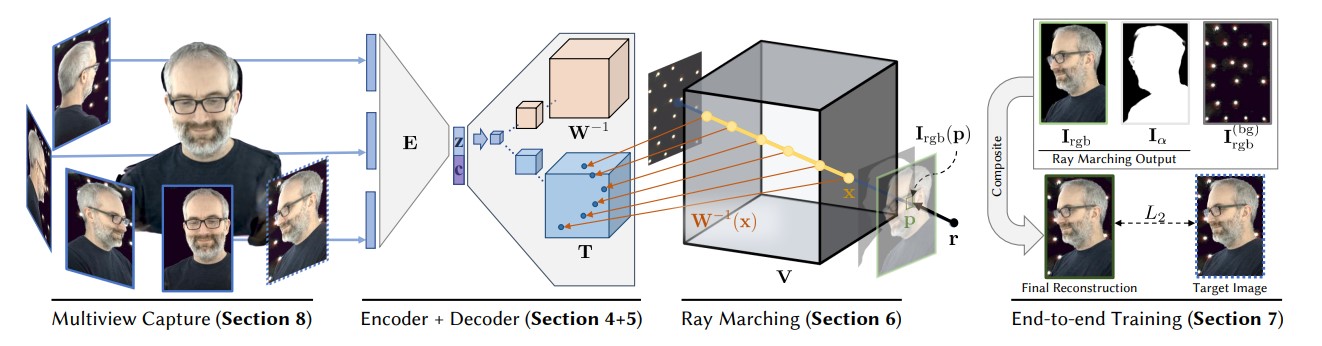
[1] Lombardi et al. - Neural Volumes: Learning Dynamic Renderable Volumes from Images - 2019

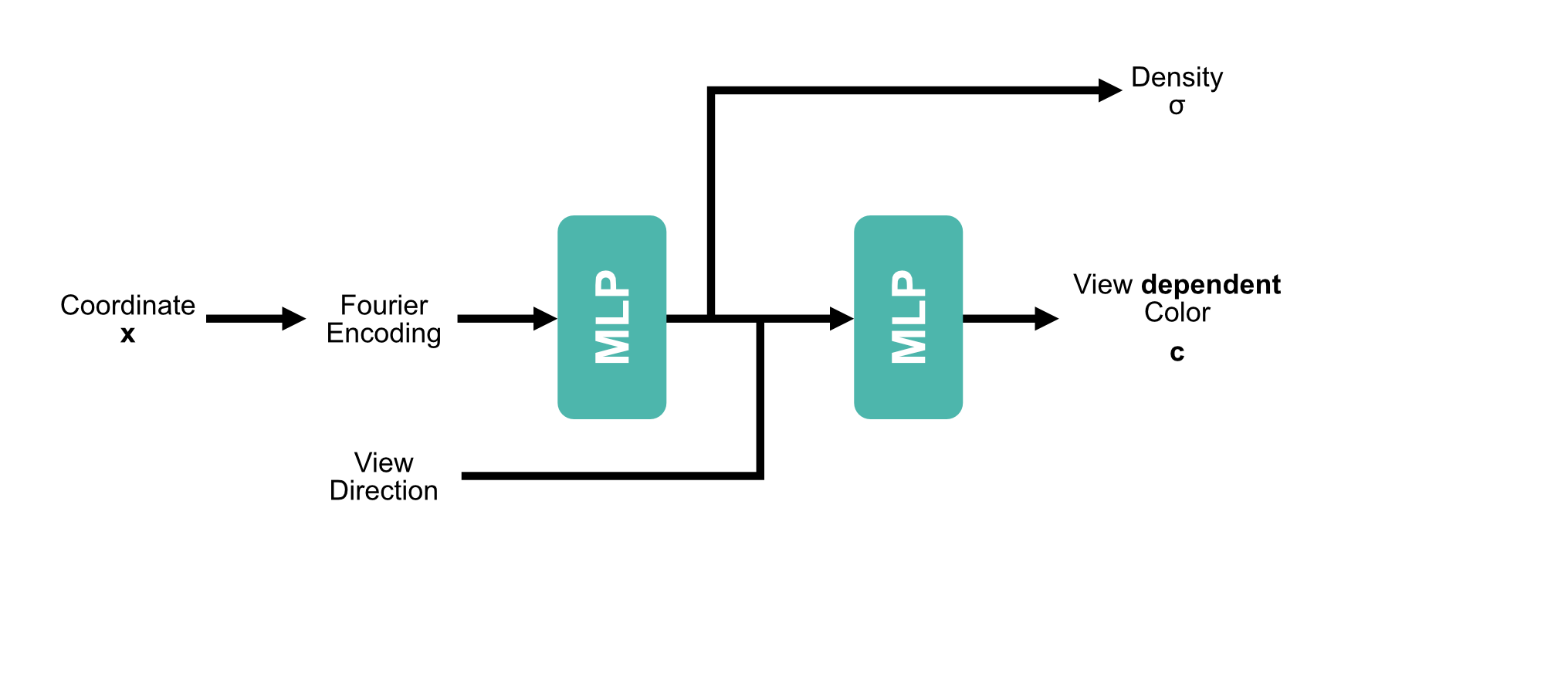
[2] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

[1] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

Learn radiance (view-dependent RGB color)
Goal is often novel view synthesis
Often neural volume rendering is used [1, 2, 3]
Can be extended with GLO embeddings to multiple illuminations [3]

Novel view synthesis with NeRF [1]

[1] Lombardi et al. - Neural Volumes: Learning Dynamic Renderable Volumes from Images - 2019

[2] Mildenhall et al. - NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - 2020

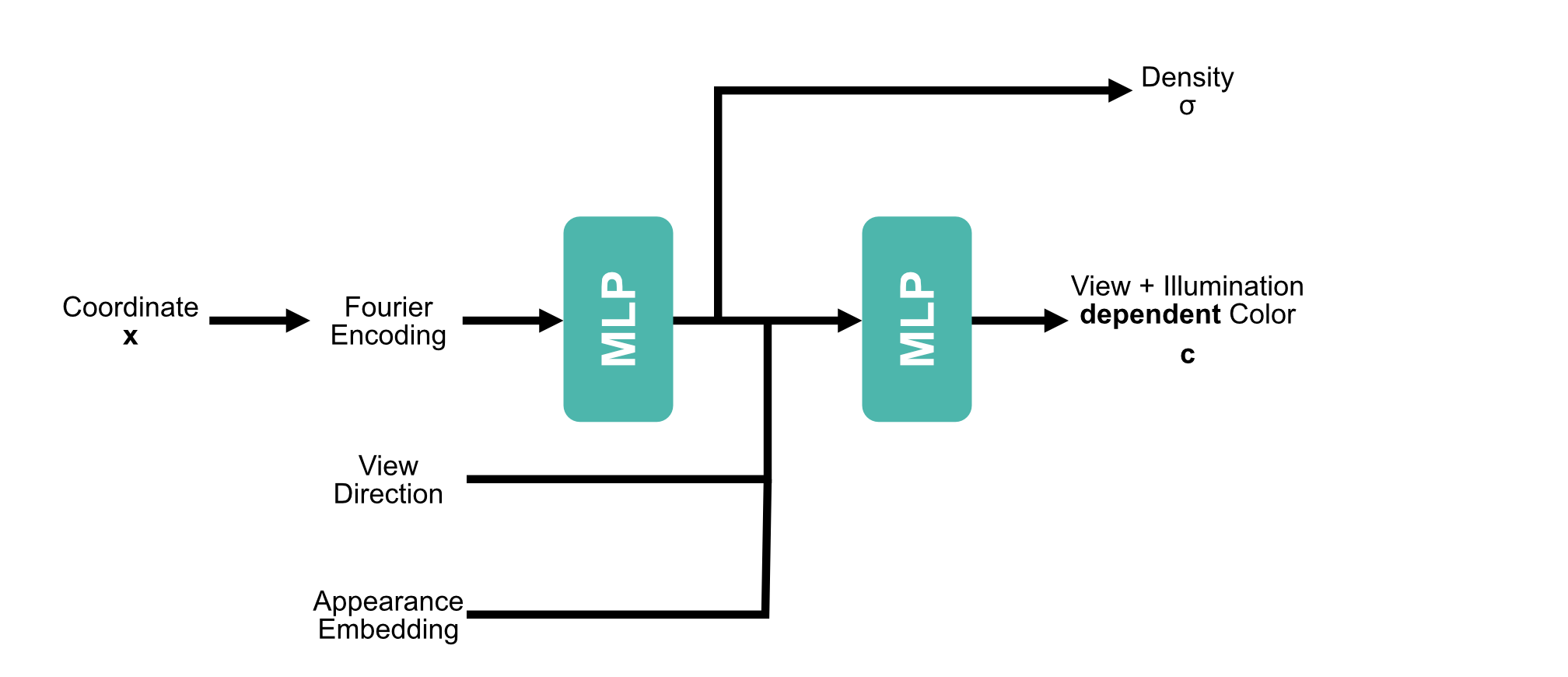
[3] Martin-Brualla et al. - NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections - 2021

Decompose the rendering equation into geometry, illumination & reflectance
Neural volume rendering (NeRF-style) used [1, 2, 3, 4]
Can be also used to decompose a trained NeRF model [3]
Specialized methods exist which directly optimize assets [4]
Related works focus on single illumination per object

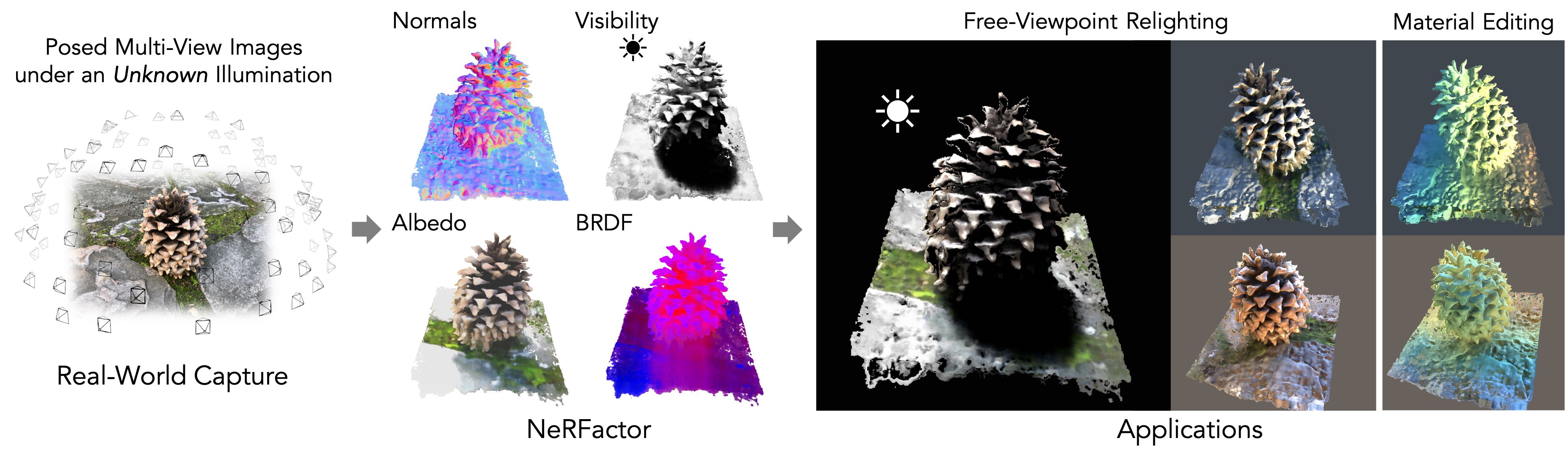
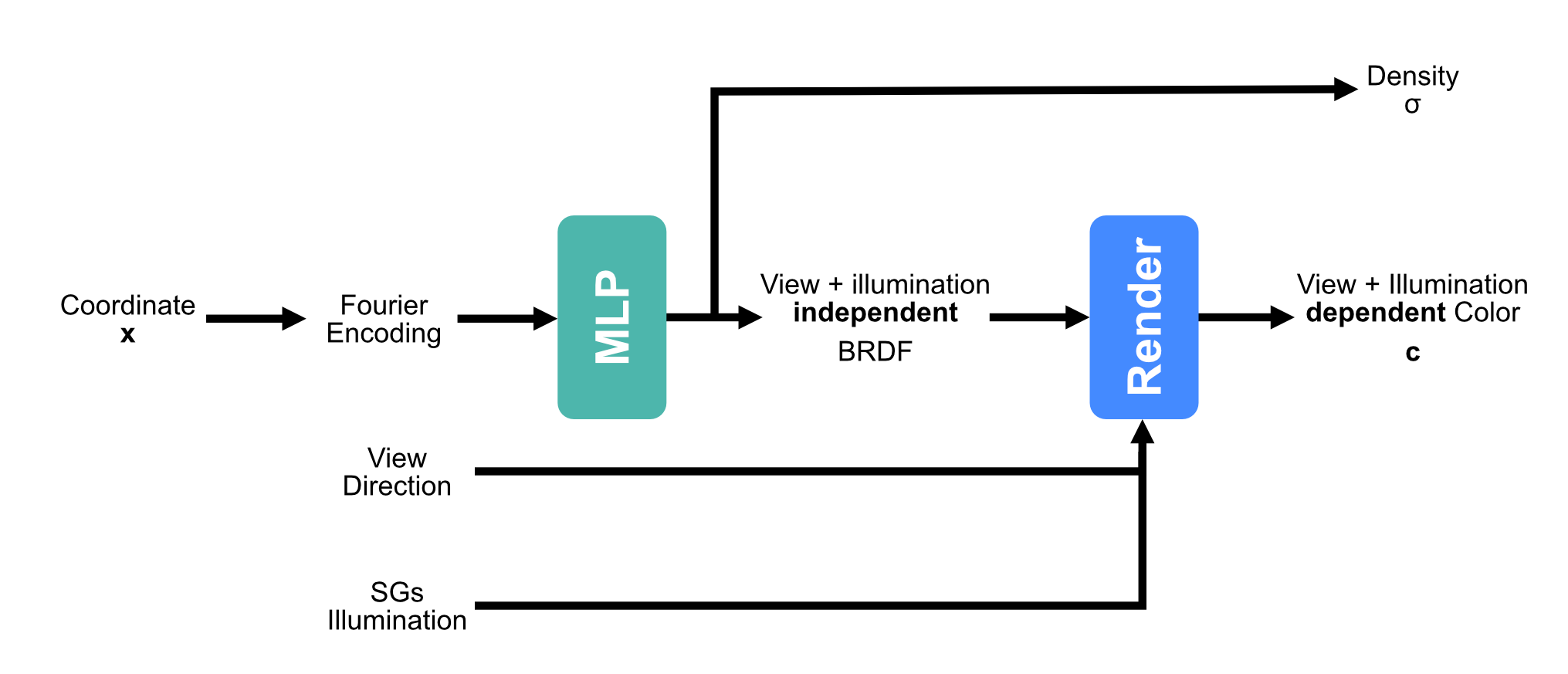
[1] Zhang et al. - PhySG: Inverse Rendering with Spherical Gaussians for Physics-based Material Editing and Relighting - 2021

[2] Srinivasan et al. - NeRV: Neural Reflectance and Visibility Fields for Relighting and View Synthesis - 2021

[3] Zhang et al. - NeRFactor: Neural Factorization of Shape and Reflectance Under an Unknown Illumination - 2021

[4] Munkberg et al. - Extracting Triangular 3D Models, Materials, and Lighting From Images - 2022

Spherical Gaussian (SG) have convenient properties
Close-form solution exists for integration 2 SGs
Product of 2 SGs is a SG

Represent illumination as SG
Simpler differentiation
- No sampling noise compared to Monte Carlo integration

Extracting textured meshes allows multiple use cases

Synthetic scenes - PSNR
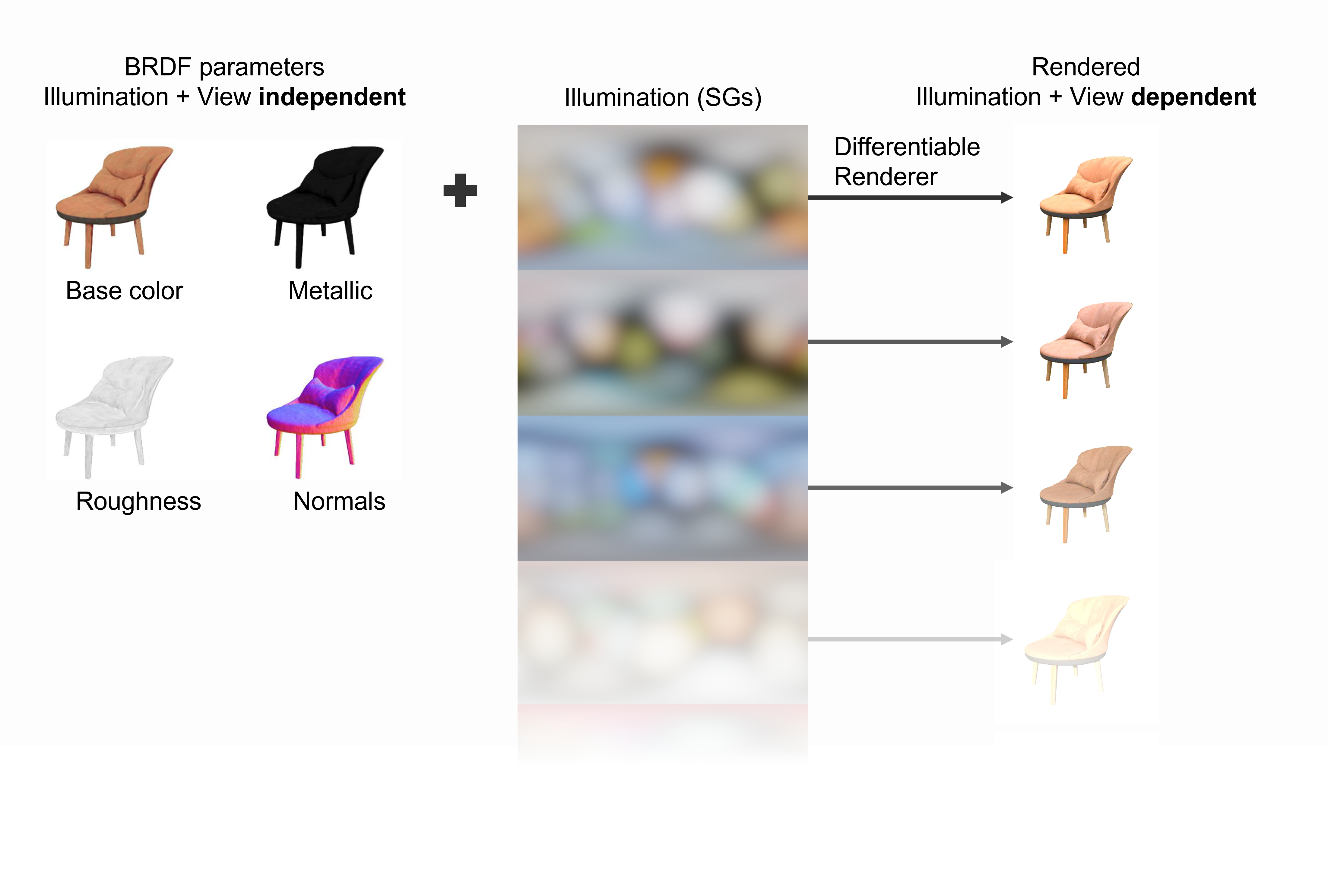
Method	Single	Multiple
NeRF	34.24	21.05
NeRF-A	32.44	28.53
NeRD (Ours)	30.07	27.96

Real world scenes - PSNR
Method	Single	Multiple
NeRF	23.34	20.11
NeRF-A	22.87	26.36
NeRD (Ours)	23.86	25.81

Learn a smooth low-dimensional manifold to represent BRDF and lighting
Constraints BRDF and light to plausible values
Auto-encoder learning with interpolated latent space
Smooth manifold losses include:
- Adversarial
- Gradient regularization during manifold interpolation

Pre-compute light integrals for fast rendering

$L_o(x,\omega_o) = \underbrace{\frac{c_d}{\pi} \int_\Omega L_i(x, \omega_i) (\omega_i \cdot n) d\omega_i}_{\text{Diffuse}} + \underbrace{\int_\Omega f_r(x,\omega_i,\omega_o; c_s, c_r) L_i(x, \omega_i)(\omega_i \cdot n) d\omega_i}_{\text{Specular}}$

$L_o(x,\omega_o) = \underbrace{\frac{c_d}{\pi} \color{red}\boxed{\color{black}\int_\Omega L_i(x, \omega_i)}\color{black} (\omega_i \cdot n) d\omega_i}_{\text{Diffuse}} + \underbrace{\color{red}\boxed{\color{black}\int_\Omega}\color{black} f_r(x,\omega_i,\omega_o; c_s, c_r) \color{red}\boxed{\color{black}L_i(x, \omega_i)}\color{black} (\omega_i \cdot n) d\omega_i}_{\text{Specular}}$

Pre-integrated light formulation

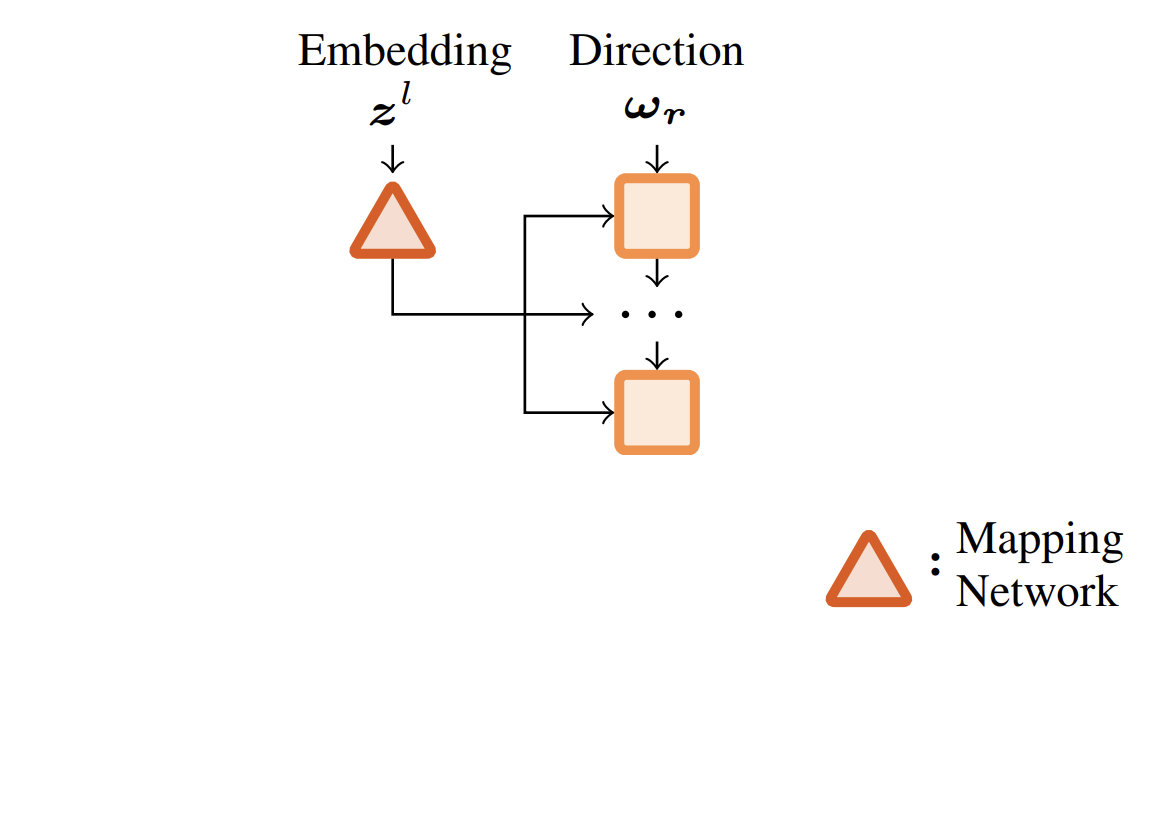
$\color{red}\boxed{\color{black}\tilde{L}_i(\omega_r, c_r)}\color{black} = \int_\Omega D(c_r, \omega_i, \omega_r)L_i(x, \omega_i)d\omega_i$

Pre-integrated rendering equation

$L_o(x,\omega_o) \approx \underbrace{\frac{c_d}{\pi} \tilde{L}_i(n, 1)}_{\text{Diffuse}} + \underbrace{b_s (F_0(\omega_o,n)B_0(\omega_o \cdot n, c_r) + B_1(\omega_o \cdot n, c_r)) \tilde{L}_i(\omega_r, c_r)}_{\text{Specular}}$

[1] Karis et al. - Real Shading in Unreal Engine 4

Light pre-integration is still expensive
We need to do the pre-integration on the fly
Neural-PIL that converts light pre-integration into a simple network query
Architecture based on pi-GAN [1]

Light Pre-integration Equation:

$\tilde{L}_i(\omega_r, c_r) = \int_\Omega D(c_r, \omega_i, \omega_r)L_i(x, \omega_i)d\omega_i$

Evaluation time
Rendering	SGs	Neural PIL
1 Million Samples	0.21s	0.00186s

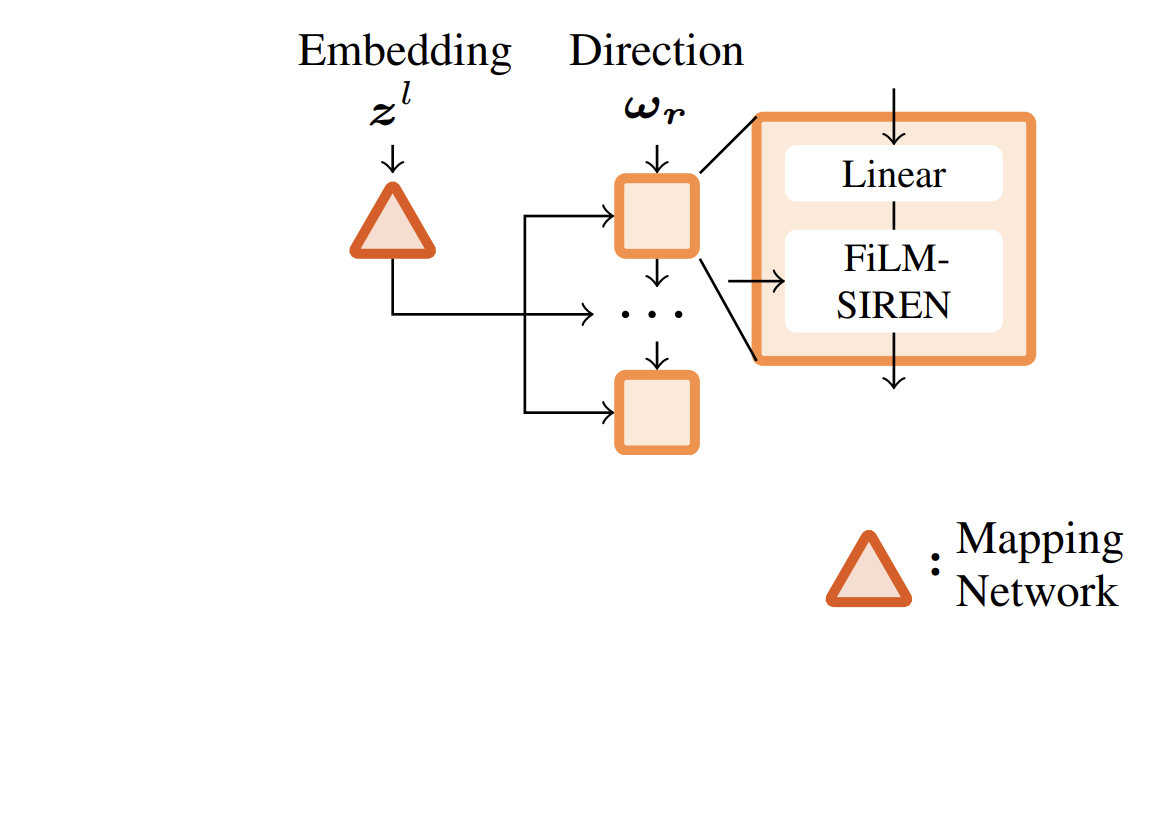
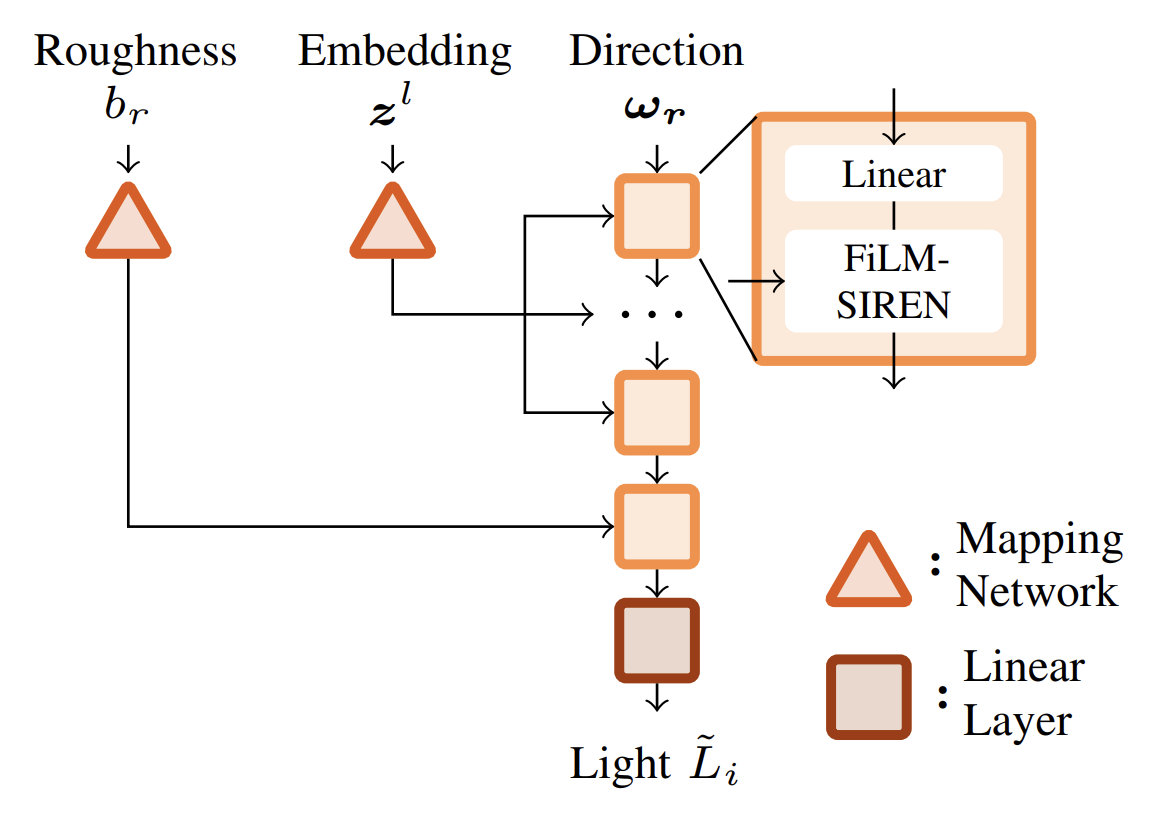
[1] Chan et al. – pi-GAN: Periodic Implicit Generative Adversarial Networks for 3D-Aware Image Synthesis - 2021

Examplary input

Examplary input

Examplary input

Synthetic scenes - PSNR
Method	Single	Multiple
NeRF	34.24	21.05
NeRF-A	32.44	28.53
NeRD (Ours)	30.07	27.96
Neural-PIL (Ours)	30.08	29.24

Real world scenes - PSNR
Method	Single	Multiple
NeRF	23.34	20.11
NeRF-A	22.87	26.36
NeRD (Ours)	23.86	25.81
Neural-PIL (Ours)	23.95	26.23

Optimize camera parameters, neural reflectance field, and illumination

BARF-style Fourier Encoding Annealing
Gradual increase in resolution
Multiple camera estimates

Posterior scaling also applied on image level
Influence of badly aligned images or segmentation masks reduced

Influence of poorly aligned images is reduced

BARF

SAMURAI

Frozen position with view conditioning

BARF

SAMURAI

Single Illumination
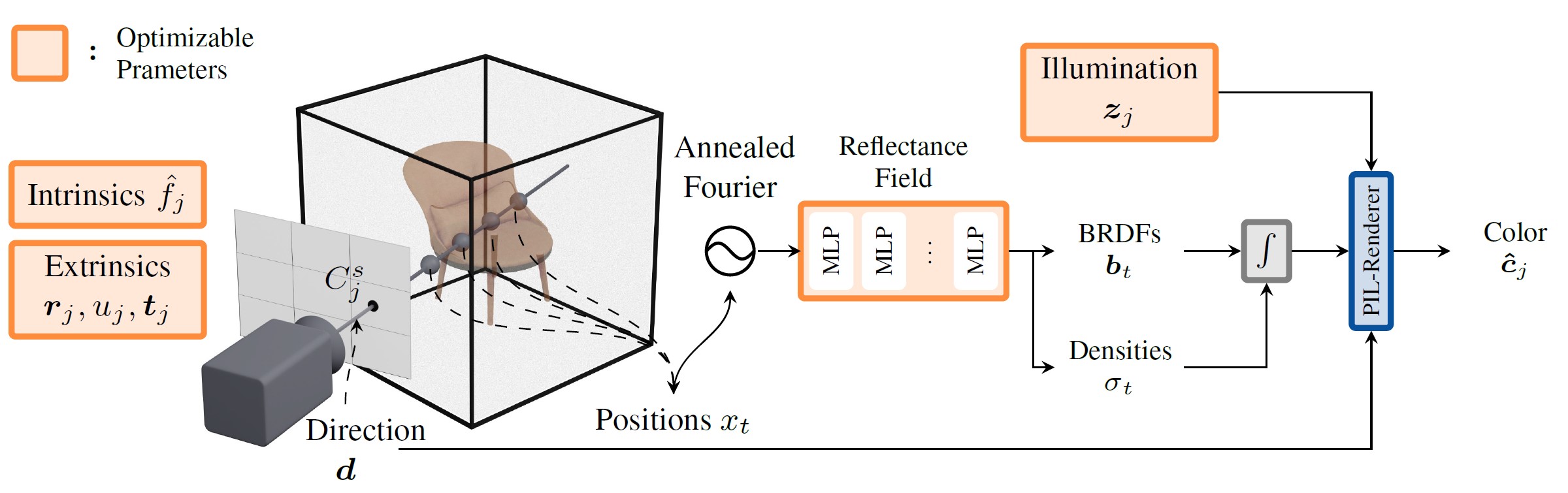
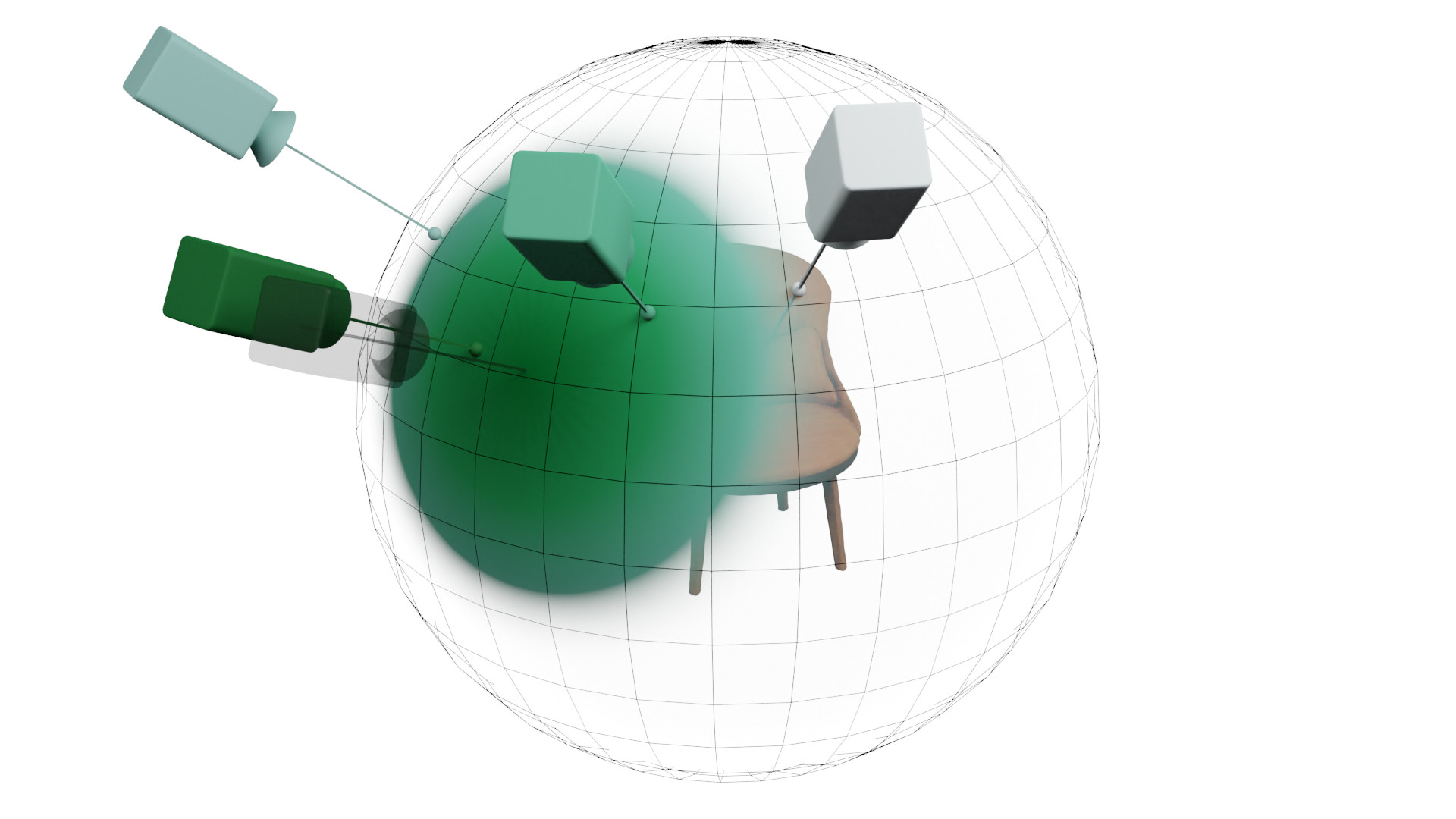
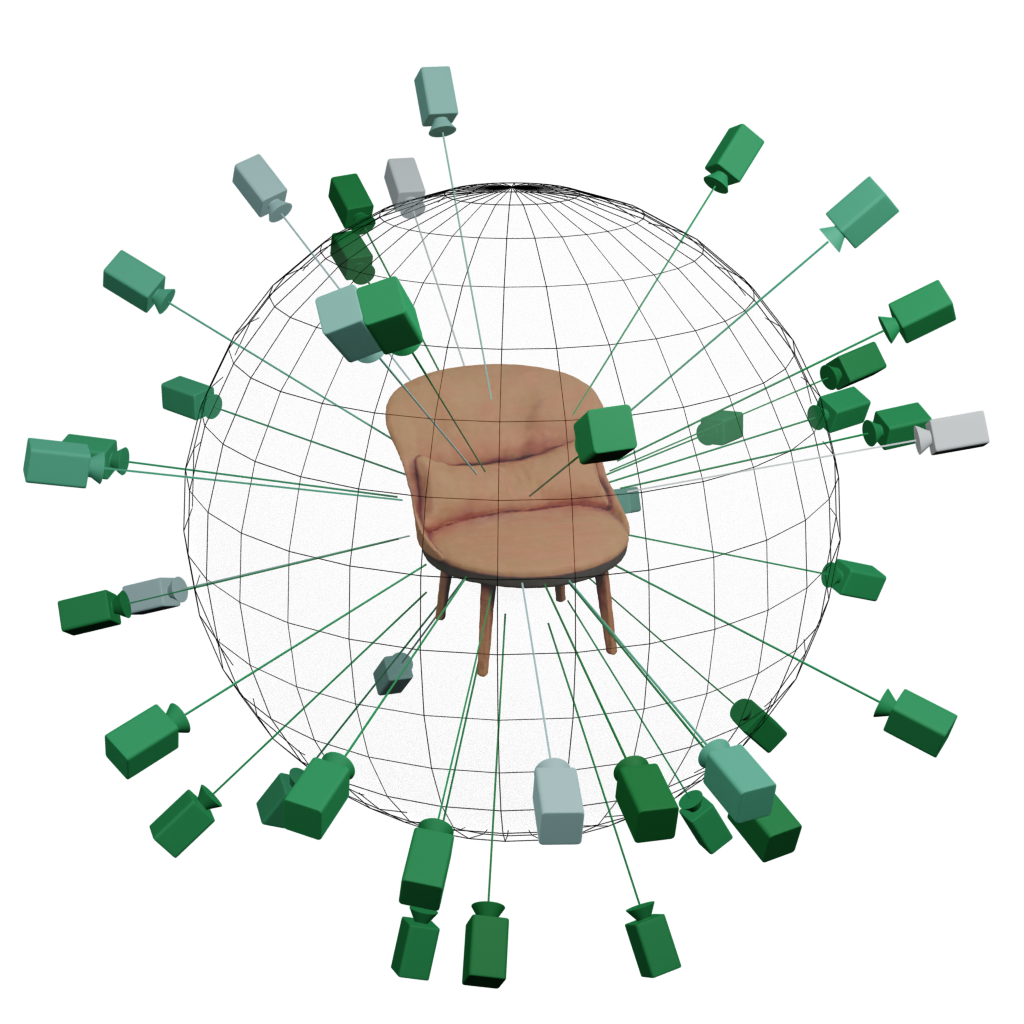
Method	Pose Init	PSNR ↑	Translation Error ↓	Rotation° Error ↓
BARF [1]	Directions	14.96	34.64	0.86
GNeRF [2]	Random	20.3	81.22	2.39
NeRS [3]	Directions	12.84	32.77	0.77
SAMURAI	Directions	21.08	33.95	0.71
NeRD	GT	23.86	—	—
Neural-PIL	GT	23.95	—	—

[1] Lin et al. - BARF: Bundle-adjusting neural radiance fields

[2] Meng et al. - GNeRF: GAN-based Neural Radiance Field without Posed Camera

[3] Zhang et al. - NeRS: Neural reflectance surfaces for sparse-view 3d reconstruction in the wild

Dataset with poses available (NeRD datasets)
Method	Pose Init	PSNR ↑	Translation Error ↓	Rotation° Error ↓
BARF-A	Directions	19.7	23.38	2.99
SAMURAI	Directions	22.84	8.61	0.89
NeRD	GT	26.88	—	—
Neural-PIL	GT	27.73	—	—

New SAMURAI datasets (No poses recoverable)
Method	Pose Init	PSNR ↑
BARF-A	Directions	16.9
SAMURAI	Directions	23.46

Solving the inverse rendering problem is highly ill-posed

We presented three novel methods of solving this task from image collections
NeRD and Neural-PIL requires posed image collections

Neural-PIL introduces general priors guiding the estimation
- Prior knowledge from datasets for BRDF and illumination
- Optimized to specific scene
- Outperforms prior art

SAMURAI does not require poses and can work on datasets which COLMAP cannot handle
- The explicit BRDF decomposition is beneficial

Create 3D assets from unconstrained input data

Turn online searches into relightable 3D objects

SAMURAI takes first steps toward that goal

Manually created 3D model

Currently only static scenes
Even scenes without humans move due to wind (Trees)
NeRFies [1] or HyperNeRF [2] bend the ray based on the time step
Both NeRFies and HyperNeRF only output the radiance

Nerfies bend the ray for the volume sampling [1]

Result from Nerfies[1]

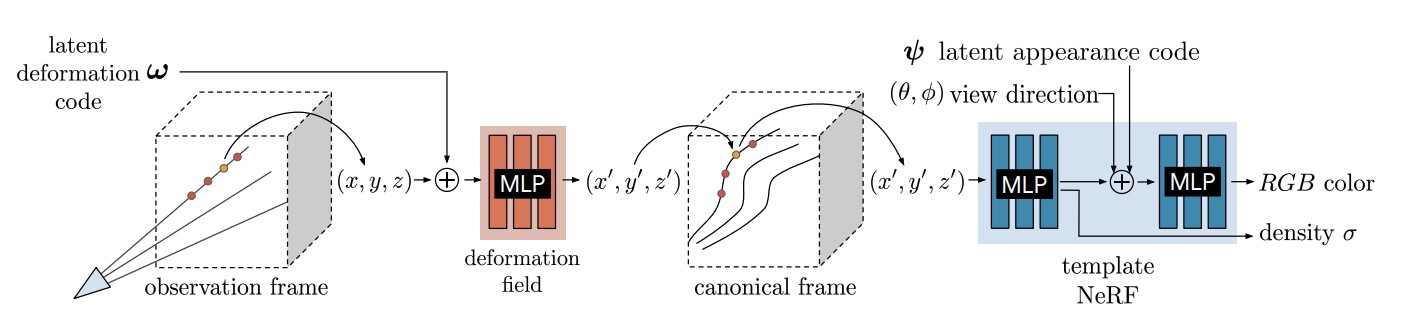
[1] Park et al. - Nerfies: Deformable Neural Radiance Fields - 2021

[2] Park et al. - A Higher-Dimensional Representation for Topologically Varying Neural Radiance Fields - 2021

Decompose rooms or large buildings (churches)
Illumination is not global and inter-reflections play a large role
Modeling dynamic movement of foliage is important
BlockNeRF only models radiance

Result from Block-NeRF[1]

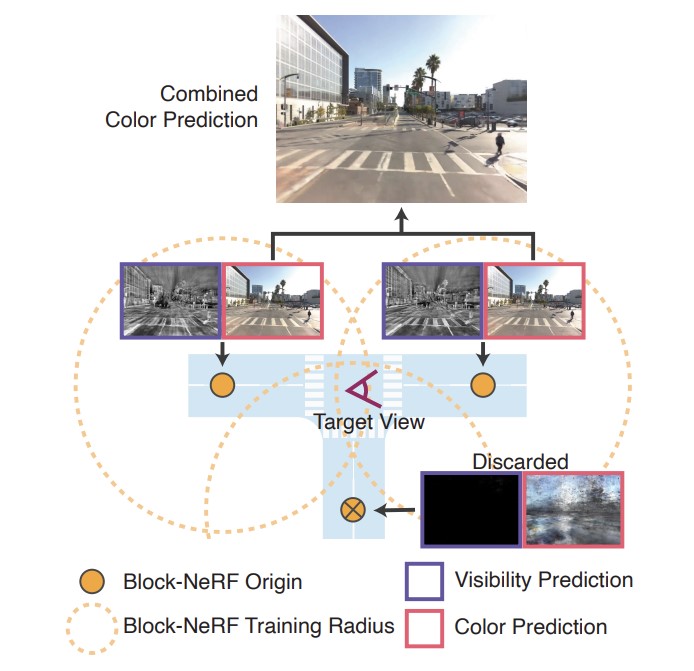
[1] Tancik et al. - Block-NeRF: Scalable Large Scene Neural View Synthesis - 2022

SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections

Mark Boss, Andreas Engelhardt, Abhishek Kar, Yuanzhen Li, Deqing Sun, Jonathan T. Barron, Hendrik P. A. Lensch, Varun Jampani - Under Submission - 2022

Medicine quality screening: TLCyzer, an open-source smartphone-based imaging algorithm for quantitative evaluation of thin-layer chromatographic analyses using the GPHF Minilab

Cathrin Hauk, Mark Boss, Julia Gabel, Simon Schäfermann, Hendrik P. A. Lensch, Lutz Heide - Under Submission - 2022

Neural-PIL: Neural Pre-Integrated Lighting for Reflectance Decomposition

Mark Boss, Varun Jampani, Raphael Braun, Ce Liu, Jonathan T. Barron, Hendrik P. A. Lensch - Advances in Neural Information Processing Systems - 2021

NeRD: Neural Reflectance Decomposition from Image Collections

Mark Boss, Raphael Braun, Varun Jampani, Jonathan T. Barron, Ce Liu, Hendrik P. A. Lensch - IEEE International Conference on Computer Vision - 2021

Two-shot Spatially-varying BRDF and Shape Estimation

Mark Boss, Varun Jampani, Kihwan Kim, Hendrik P. A. Lensch, Jan Kautz - IEEE Conference on Computer Vision and Pattern Recognition - 2020

Single Image BRDF Parameter Estimation with a Conditional Adversarial Network

Mark Boss, Hendrik P. A. Lensch - ArXiv - 2019

Deep Dual Loss BRDF Parameter Estimation

Mark Boss, Fabian Groh, Sebastian Herholz, Hendrik P. A. Lensch - Workshop on Material Appearance Modeling - 2018