Neural-PIL: Neural Pre-Integrated Lighting for Reflectance Decomposition

Introduction

Besides the general NeRF Explosion of 2020, a subfield of introducing explicit material representations in to neural volume representation emerged with papers such as NeRD, NeRV, Neural Reflectance Fields for Appearance Acquisition, PhySG or NeRFactor. The way illumination is represented varies drastically between the methods. Either the methods focus on single-point lights such as in Neural Reflectance Fields for Appearance Acquisition, it is assumed to be known (NeRV), it is extracted from a trained NeRF as an illumination map (NeRFactor), or it is represented as Spherical Gaussians (NeRD and PhySG). It is also worth pointing out that nearly all methods focus on a single illumination per scene, except NeRD.

While NeRD enabled decomposition from multiple views under different illumination, SGs only allowed for rather diffuse illuminations. Inspired from Pre-integrated Lighting from real-time rendering, we transfer this concept to a neural network, which handles the integration and can represent illuminations from a manifold of natural illuminations.

Method

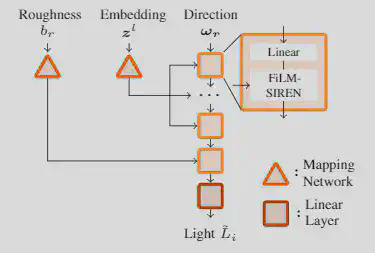
In FIGURE 1 visualizes the Neural-PIL architecture, which is inspired by pi-GAN. As seen, the mapping networks are used on the embedding $z^l$, which describes the general content of the environment map and the roughness $b_r$, which defines how rough and therefore how blurry the environment should be.

Visually this can be seen in FIGURE 2. If the BRDF, shown on the left for each pair, becomes rougher, the illuminations from a larger area get integrated. The result is a blurrier environment map.

As a joint decomposition of illumination, shape, and appearance is a challenging, ill-posed task, we introduce priors to the BRDF and illumination. The illumination should only lie on a smooth manifold of natural illumination and the BRDF on possible materials. Here, we introduce a Smooth Manifold Auto-Encoder (SMAE).

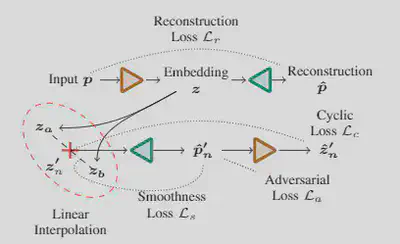
Inspired by Berthelot et al. - Understanding and Improving Interpolation in Autoencoders via an Adversarial Regularizer, we introduce the interpolation in latent space during training, we further introduce three additional losses which further aid in a smooth manifold formation. The smoothness loss encourages a smooth gradient w.r.t. to the interpolation factor and therefore achieves a smooth interpolation between two points in the latent space. The cyclic loss enforces that the encoder and decoder perform the same step by re-encoding the decoded interpolated embeddings and ensuring the re-encoded latent vectors are the same as the initial ones. Lastly, we add a discriminator trained on the examples from the dataset as real ones and the interpolated ones as fake and try to fool it with our interpolated embeddings. With these three losses, a smooth latent space is formed, which allows for an easy introduction in our framework, where the corresponding networks are frozen, and only the latent space is optimized.