NeRD: Neural Reflectance Decomposition from Image Collections

Mark Boss, Raphael Braun, Varun Jampani, Jonathan T. Barron, Ce Liu, Hendrik P. A. Lensch

November, 2020

Overview of the method. NeRD decomposes a scene from multiple input images into a neural volume with explicit BRDFs. The information can be extracted to traditional textured meshes.

Abstract

Decomposing a scene into its shape, reflectance, and illumination is a challenging but important problem in computer vision and graphics. This problem is inherently more challenging when the illumination is not a single light source under laboratory conditions but is instead an unconstrained environmental illumination. Though recent work has shown that implicit representations can be used to model the radiance field of an object, most of these techniques only enable view synthesis and not relighting. Additionally, evaluating these radiance fields is resource and time-intensive. We propose a neural reflectance decomposition (NeRD) technique that uses physically-based rendering to decompose the scene into spatially varying BRDF material properties. In contrast to existing techniques, our input images can be captured under different illumination conditions. In addition, we also propose techniques to convert the learned reflectance volume into a relightable textured mesh enabling fast real-time rendering with novel illuminations. We demonstrate the potential of the proposed approach with experiments on both synthetic and real datasets, where we are able to obtain high-quality relightable 3D assets from image collections.

Type

Conference paper

Publication

In IEEE International Conference on Computer Vision

Introduction

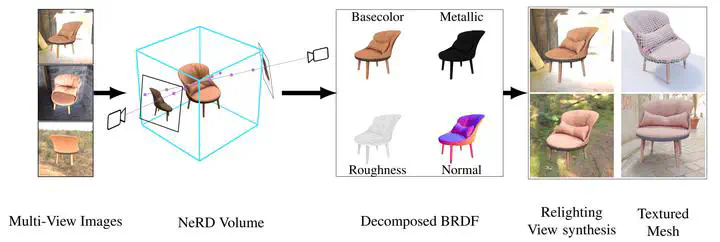
NeRD is a novel method that can decompose image collections from multiple views taken under varying or fixed illumination conditions. The object can be rotated, or the camera can turn around the object. The result is a neural volume with an explicit representation of the appearance and illumination in the form of the BRDF and Spherical Gaussian (SG) environment illumination.

The method is based on the general structure of NeRF. However, NeRF encodes the scene to an implicit BRDF representation where a Multi-Layer-Perceptron (MLP) is queried for outgoing view directions at every point. Extracting information from NeRF is therefore not easily done, and the inference time for novel views takes around 30 seconds. Also, NeRF is not capable of relighting an object under any illumination. By introducing physically-based representations for lighting and appearance, NeRD can relighting an object, and information can be extracted from the neural volume. After our extraction process, the result is a regular texture mesh that can be rendered in real-time. See our results where we provide a web-based interactive renderer.

Method

Decomposing the scene requires that the integral over the hemisphere from the rendering equation is decomposed into its parts. Here, we use a simplified version without self-emittance. $$L_o(x,\omega_o) = \int_\Omega L_i(x,\omega_i) f_r(x,\omega_i,\omega_o) (\omega_i \cdot n) d\omega_i$$ Here, $L_o$ is the outgoing radiance for a point $x$ in the direction $\omega_o$. This radiance is calculated by integrating all influences over the hemisphere $\Omega$, which are based on the incoming light $L_i$ for each direction $\omega_i$. The surface behavior is expressed as the BRDF $f_r$, which describes how incoming light $\omega_i$ is directed to the outgoing direction $\omega_o$. Lastly, a cosine term is used $(\omega_i \cdot n)$, which reduces the received light based on the angle towards the light source.

The inverse of this integral is highly ambiguous, and we use several approximations to solve it. We do not use any interreflections or shadowing, which means that we do not compute the incoming radiance recursively. Additionally, our illumination is expressed as SG, which reduces a full continuous integral to - in our case - 24 evaluation of the environment SGs.

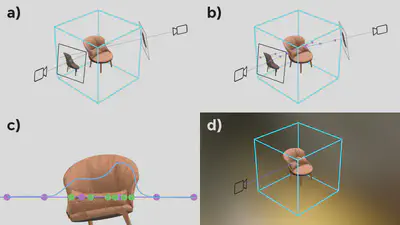
Steps of the query process. In a) the volume is constructed by tracing rays from each camera into the scene. Then samples are placed along with the rays in b), and based on the density at each sampling point, additional samples are placed in c). The samples are then evaluated into a BRDF, which is re-rendered using the jointly optimized illumination in d).

Inspired by NeRF the method uses two MLPs, which encode the each position in the volume $\textbf{x} = (x,y,z)$ to a volume density $\sigma$ and a color or BRDF parameters. Figure 1 shows an overview of this optimization process.

Results

Click the images for an interactive 3D visualization.

Real-world

Real-world (Preliminary in the wild)

The images from the Statue of Liberty are collected from Flickr, Unsplash, Youtube and Vimeo videos. In total about 120 images are used for training from various phones, cameras and drones. Overall even the COLMAP registration is not perfect due to the simplistic shared camera model.

Synthetic Examples

Copyright

This material is posted here with permission of the IEEE. Internal or personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution must be obtained from the IEEE by writing to pubs-permissions@ieee.org.